题目内容
11.函数y=$\frac{1}{2}$tan(2x+$\frac{π}{3}$)+1的图象的对称中心为($\frac{1}{4}kπ-\frac{π}{6}$,1),k∈Z..分析 根据正切函数的性质可得答案.
解答 解:由正切函数的性质可得:2x+$\frac{π}{3}$=$\frac{π}{2}k$,k∈Z,
可得:x=$\frac{1}{4}kπ-\frac{π}{6}$,
函数y=$\frac{1}{2}$tan(2x+$\frac{π}{3}$)+1的图象的对称中心为($\frac{1}{4}kπ-\frac{π}{6}$,1),k∈Z.
故答案为:($\frac{1}{4}kπ-\frac{π}{6}$,1),k∈Z.
点评 本题主要考查正切函数的图象和性质.属于基础题.

练习册系列答案
相关题目
8.已知集合A={x|0<x<2},B={x|x2-1<0},则A∪B=( )
| A. | (-1,1) | B. | (-1,2) | C. | (1,2) | D. | (0,1) |
6.z=3-4i,则复数z-|z|+(1-i)在复平面内的对应点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
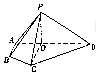 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,O为为AD上的一点,且AB⊥AD,CO⊥AD,AB=AO=$\frac{1}{3}$AD=$\frac{1}{2}$OC=1,OP=$\frac{1}{2}$CD,PA=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,O为为AD上的一点,且AB⊥AD,CO⊥AD,AB=AO=$\frac{1}{3}$AD=$\frac{1}{2}$OC=1,OP=$\frac{1}{2}$CD,PA=$\sqrt{3}$.