题目内容
已知两同心圆的半径之比为1：2，若在大圆内任取一点P，则点P在小圆内的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：几何概型
专题：概率与统计
分析：根据几何概型的概率求法，所求就是两个圆的面积比．
解答：
解：由题意，设小圆半径为r，大圆半径为2r，所以小圆面积为πr2，大圆的面积为4πr2，
所以在大圆内任取一点P，则点P在小圆内的概率为
=
；
故选C．
所以在大圆内任取一点P，则点P在小圆内的概率为
| πr2 |
| 4πr2 |
| 1 |
| 4 |
故选C．
点评：本题考查了几何概型的求法；关键是利用事件表示的长度、面积或者体积的比表示概率．
练习册系列答案
相关题目
已知两个变量x，y具有线性相关关系，并测得（x，y）的四组值分别是（2，3）、（5，7）、（8，9）、（11，13），则求得的线性回归方程所确定的直线必定经过点（ ）
| A、（2，3） |
| B、（8，9） |
| C、（6，9） |
| D、（6.5，8） |
已知Sn是等差数列{an}n∈N*的前n项和，且S6＞S7＞S5，给出下列五个命题：
①d＜0；②S11＞0；③S12＜0；④数列{Sn}中最大项为S11；⑤|a6|＞|a7|，
其中正确命题的个数（ ）
①d＜0；②S11＞0；③S12＜0；④数列{Sn}中最大项为S11；⑤|a6|＞|a7|，
其中正确命题的个数（ ）
| A、5 | B、4 | C、3 | D、1 |
函数f（x）=ax-2+loga（x-1）（a＞0且a≠1），在x∈[2，3]上的最大值与最小值之和为a，则a等于（ ）
| A、4 | ||
B、
| ||
| C、2 | ||
D、
|
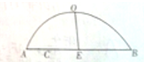如图，A处为我军一炮兵阵地，距A处1000米的C处有一小山，山高为580米，在山的另一侧距C处3000米有敌武器库B，且A、B、C在同一水平直线删个，已知我炮兵轰击敌武器库是一段抛物线，这段抛物线的最大高度OE为800米．