题目内容
5.2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程.为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与PM2.5的数据如表:| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
| 车流量x(万辆) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5的浓度y(微克/立方米) | 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(Ⅱ)(ⅰ)利用(Ⅰ)所求的回归方程,预测该市车流量为8万辆时PM2.5的浓度;
(ⅱ)规定:当一天内PM2.5的浓度平均值在(0,50]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(50,100]内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)
参考公式:回归直线的方程是$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=$\frac{{{\sum_{i=1}^{n}x}_{i}y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
分析 (Ⅰ)根据公式求出回归系数,可写出线性回归方程;
(Ⅱ)(ⅰ)根据(Ⅰ)的性回归方程,代入x=8求出PM2.5的浓度;
(ⅱ)根据题意信息得:6x+19≤100,即x≤13.5,解得x的取值范围即可.
解答 解:(Ⅰ)由数据可得:$\overline x=\frac{1}{7}({1+2+3+4+5+6+7})=4$,…(1分)$\overline y=\frac{1}{7}({28+30+35+41+49+56+62})=43$,…(2分)
$\sum_{i=1}^7{{x_i}{y_i}}=1372$,$\sum_{i=1}^7{{x_i}^2}=140$,…(4分)
$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}=\frac{1372-1204}{140-112}=6$,…(6分)$\widehata=\overline y-\widehatb\overline x=43-4×6=19$…(7分)
故y关于x的线性回归方程为$\widehaty=6x+19$.…(8分)
(Ⅱ)(ⅰ)当车流量为8万辆时,即x=8时,$\widehaty=6×8+19=67$.
故车流量为8万辆时,PM2.5的浓度为67微克/立方米.…(10分)
(ⅱ)根据题意信息得:6x+19≤100,即x≤13.5,…(11分)
故要使该市某日空气质量为优或为良,则应控制当天车流量在13万辆以内.…(12分)
点评 本题主要考查了线性回归分析的方法,包括用最小二乘法求参数,以及用回归方程进行预测等知识,考查了考生数据处理和运算能力,属于中档题.

| A. | 12 | B. | 18 | C. | 24 | D. | 36 |
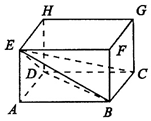 把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在长方体ABCD-EFGH中,AB=5,AD=4,AE=3,则△EBD在平面EBC上的射影的面积是( )
把平面图形M上的所有点在一个平面上的射影构成的图形M′叫作图形M在这个平面上的射影.如图,在长方体ABCD-EFGH中,AB=5,AD=4,AE=3,则△EBD在平面EBC上的射影的面积是( )| A. | 2$\sqrt{34}$ | B. | $\frac{25}{2}$ | C. | 10 | D. | 30 |
 某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于130分为优秀.
某校在一次高三年级“诊断性”测试后,对该年级的500名考生的成绩进行统计分析,成绩的频率分布表及频率分布直方图如图所示,规定成绩不小于130分为优秀.(1)若用分层抽样的方法从这500人中抽取5人的成绩进行分析,求其中成绩为优秀的学生人数;
(2)在(1)中抽取的5名学生中,要随机抽取2名学生参加分析座谈会,求恰有1人成绩为优秀的概率.
| 区间 | 人数 |
| [115,120) | 25 |
| [120,125) | a |
| [125,130) | 175 |
| [130,135) | 150 |
| [135,140) | b |
| A. | 32 | B. | 39 | C. | 46 | D. | 78 |