题目内容
15.在等差数列{an}中,若a3+a11=6,则其前13项的和S13的值是( )| A. | 32 | B. | 39 | C. | 46 | D. | 78 |
分析 由等差数列前n项和公式及通项公式得S13=$\frac{13}{2}({a}_{3}+{a}_{11})$,由此能求出结果.
解答 解:∵等差数列{an}中,a3+a11=6,
∴其前13项的和:
S13=$\frac{13}{2}({a}_{1}+{a}_{13})$=$\frac{13}{2}×6=39$.
故选:B.
点评 本题考查等差数列的前13项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
5.2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程.为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与PM2.5的数据如表:
(Ⅰ)由散点图知y与x具有线性相关关系,求y关于x的线性回归方程;
(Ⅱ)(ⅰ)利用(Ⅰ)所求的回归方程,预测该市车流量为8万辆时PM2.5的浓度;
(ⅱ)规定:当一天内PM2.5的浓度平均值在(0,50]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(50,100]内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)
参考公式:回归直线的方程是$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=$\frac{{{\sum_{i=1}^{n}x}_{i}y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
| 车流量x(万辆) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5的浓度y(微克/立方米) | 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(Ⅱ)(ⅰ)利用(Ⅰ)所求的回归方程,预测该市车流量为8万辆时PM2.5的浓度;
(ⅱ)规定:当一天内PM2.5的浓度平均值在(0,50]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(50,100]内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)
参考公式:回归直线的方程是$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=$\frac{{{\sum_{i=1}^{n}x}_{i}y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
6.若平面α,β,γ中,α⊥β,则“γ⊥β”是“α∥γ”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
3.已知抛物线C:y2=8x,直线l:y=$\frac{{\sqrt{3}}}{3}$(x-2),直线l交C于A,B两点,则|AB|等于( )
| A. | 16 | B. | $16\sqrt{3}$ | C. | 32 | D. | $32\sqrt{3}$ |
20.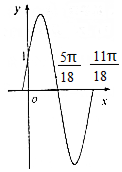 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{5π}{9}$)的值是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{5π}{9}$)的值是( )
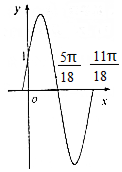 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{5π}{9}$)的值是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{5π}{9}$)的值是( )| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
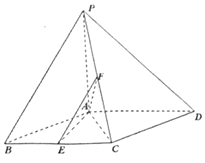 已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC中点.
已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC中点.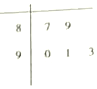 2017年2月20日,摩拜单车在济南推出“做文明骑士,周一摩拜单车免费骑”活动,为了解单车使用情况,记者随机抽取了五个投放区域,统计了半小时内被骑走的单车数量,绘制了如图所示的茎叶图,则该组数据的方差为( )
2017年2月20日,摩拜单车在济南推出“做文明骑士,周一摩拜单车免费骑”活动,为了解单车使用情况,记者随机抽取了五个投放区域,统计了半小时内被骑走的单车数量,绘制了如图所示的茎叶图,则该组数据的方差为( )