题目内容
17.若实数x,y满足$\left\{\begin{array}{l}{y≥0}\\{x+y≤0}\\{2x+y+2≥0}\end{array}\right.$,则z=2x-y的最小值为-6.分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.
解答 解:由约束条件作出可行域:
联立$\left\{\begin{array}{l}{x+y=0}\\{2x+y+2=0}\end{array}\right.$,解得A(-2,2),
化z=2x-y为y=2x-z,由图可知,当直线y=2x-z过A时,直线在y轴上的截距最大,z有最小值为-6.
故答案为:-6.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
5.2015年12月,京津冀等地数城市指数“爆表”,北方此轮污染为2015年以来最严重的污染过程.为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与PM2.5的数据如表:
(Ⅰ)由散点图知y与x具有线性相关关系,求y关于x的线性回归方程;
(Ⅱ)(ⅰ)利用(Ⅰ)所求的回归方程,预测该市车流量为8万辆时PM2.5的浓度;
(ⅱ)规定:当一天内PM2.5的浓度平均值在(0,50]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(50,100]内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)
参考公式:回归直线的方程是$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=$\frac{{{\sum_{i=1}^{n}x}_{i}y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期七 |
| 车流量x(万辆) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| PM2.5的浓度y(微克/立方米) | 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(Ⅱ)(ⅰ)利用(Ⅰ)所求的回归方程,预测该市车流量为8万辆时PM2.5的浓度;
(ⅱ)规定:当一天内PM2.5的浓度平均值在(0,50]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(50,100]内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)
参考公式:回归直线的方程是$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=$\frac{{{\sum_{i=1}^{n}x}_{i}y}_{i}-n\overline{x}\overline{y}}{{\sum_{i=1}^{n}x}_{i}^{2}-{n\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
12.设i为虚数单位,则$\frac{3-i}{i}$=( )
| A. | -1-3i | B. | 1-3i | C. | -1+3i | D. | 1+3i |
9.已知实数x,y满足$\left\{\begin{array}{l}{y≥0}\\{x+y≤0}\\{2x+y+2≤0}\end{array}\right.$且ax-y+1-a=0,则实数a的取值范围是( )
| A. | [-$\frac{1}{3}$,1) | B. | [-1,$\frac{1}{2}$] | C. | (-1,$\frac{1}{2}$] | D. | [-$\frac{1}{3}$,$\frac{1}{2}$] |
6.若平面α,β,γ中,α⊥β,则“γ⊥β”是“α∥γ”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
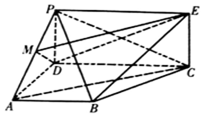 如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.
如图,四边形PDCE为矩形,四边形ABCD为梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=1.