题目内容
观察下列不等式:
<
,
<
,
<
,
<
,…
照此规律,写出第n个不等式,然后判断这个不等式是否成立并给出证明.
| 2 |
| 3 |
| 2+1 |
| 3+1 |
| 2 |
| 3 |
| 2+2 |
| 3+2 |
| 2 |
| 3 |
| 2+3 |
| 3+3 |
| 2 |
| 3 |
| 2+4 |
| 3+4 |
照此规律,写出第n个不等式,然后判断这个不等式是否成立并给出证明.
考点:归纳推理
专题:规律型
分析:根据已知中,
<
,
<
,
<
,
<
,…可猜想第n个不等式为
<
,进而利用作差法,进行证明.
| 2 |
| 3 |
| 2+1 |
| 3+1 |
| 2 |
| 3 |
| 2+2 |
| 3+2 |
| 2 |
| 3 |
| 2+3 |
| 3+3 |
| 2 |
| 3 |
| 2+4 |
| 3+4 |
| 2 |
| 3 |
| 2+n |
| 3+n |
解答:
解:根据已知中,
<
,
<
,
<
,
<
,
…
可猜想第n个不等式为
<
,
证明如下:
∵n∈N*,
∴n>0且3+n>0,
∴
-
=
=
>0,即
<
.
| 2 |
| 3 |
| 2+1 |
| 3+1 |
| 2 |
| 3 |
| 2+2 |
| 3+2 |
| 2 |
| 3 |
| 2+3 |
| 3+3 |
| 2 |
| 3 |
| 2+4 |
| 3+4 |
…
可猜想第n个不等式为
| 2 |
| 3 |
| 2+n |
| 3+n |
证明如下:
∵n∈N*,
∴n>0且3+n>0,
∴
| 2+n |
| 3+n |
| 2 |
| 3 |
| 3(2+n)-2(3+n) |
| 3(3+n) |
| n |
| 3(3+n) |
| 2 |
| 3 |
| 2+n |
| 3+n |
点评:此题主要考查了归纳推理,不等式证明,利用已知得出数字之间的规律是解决问题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
设p:“x,y,z中至少有一个等于1”?“(x-1)(y-1)(z-1)=0”;q:“
+|y-2|+(z-3)2=0”?“(x-1)(y-2)(z-3)=0”,那么p,q的真假是( )
| x-1 |
| A、p真q真 | B、p真q假 |
| C、p假q真 | D、p假q假 |
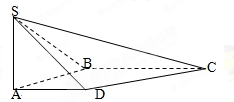 在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AD=AB=1,BC=
在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AD=AB=1,BC= 在平面直角坐标系xOy中,过点P(-4,0)作直线交椭圆C:
在平面直角坐标系xOy中,过点P(-4,0)作直线交椭圆C: