题目内容
3.已知f(x)=|ax-1|,若实数a>0,不等式f(x)≤3的解集是{x|-1≤x≤2}.(Ⅰ)求a的值;
(Ⅱ)若$\frac{f(x)+f(-x)}{3}$<|k|存在实数解,求实数k的取值范围.
分析 (Ⅰ)求出不等式的解集,根据对应关系求出a的值即可;
(Ⅱ)根据不等式的性质求出 $\frac{f(x)+f(-x)}{3}$的最小值,得到关于k的不等式,解出即可.
解答 解:(Ⅰ)由|ax-1|≤3,得-3≤ax-1≤3,解得:-2≤ax≤4,
a>0时,-$\frac{2}{a}$≤x≤$\frac{4}{a}$,
而f(x)≤3的解集是{x|-1≤x≤2},
故 $\left\{\begin{array}{l}{-\frac{2}{a}=-1}\\{\frac{4}{a}=2}\end{array}\right.$,解得:a=2;
故a=2;
(Ⅱ) $\frac{f(x)+f(-x)}{3}$=$\frac{|2x-1|+|2x+1|}{3}$≥$\frac{|2x-1-2x-1|}{3}$=$\frac{2}{3}$,
故要使 $\frac{f(x)+f(-x)}{3}$<|k|存在实数解,只需|k|>$\frac{2}{3}$,
解得k>$\frac{2}{3}$或k<-$\frac{2}{3}$,
∴实数k取值范围是(-∞,-$\frac{2}{3}$)∪($\frac{2}{3}$,+∞).
点评 本题考查了解绝对值不等式问题,考查分类讨论思想以及转化思想,是一道中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
15.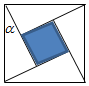 “勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角$α=\frac{π}{6}$,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是
“勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角$α=\frac{π}{6}$,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是
( )
 “勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角$α=\frac{π}{6}$,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是
“勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角$α=\frac{π}{6}$,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是( )
| A. | $1-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{4-\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
13.已知等差数列{an}的前n项和为Sn,且S6=24,S9=63,则a4=( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
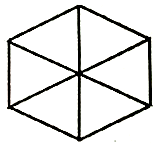 用四种不同的颜色为正六边形(如图)中的六块区域涂色,要求有公共边的区域涂不同颜色,一共有732种不同的涂色方法.
用四种不同的颜色为正六边形(如图)中的六块区域涂色,要求有公共边的区域涂不同颜色,一共有732种不同的涂色方法. 在斜三棱柱ABC-A1B1C1中,侧面AC1⊥平面ABC,$A{A_1}=\sqrt{2}a$,A1C=CA=AB=a,AB⊥AC,D是AA1的中点.
在斜三棱柱ABC-A1B1C1中,侧面AC1⊥平面ABC,$A{A_1}=\sqrt{2}a$,A1C=CA=AB=a,AB⊥AC,D是AA1的中点.