题目内容
18.已知正项数列n的前n项和为Sn,且a1=1,an+12=Sn+1+Sn.(1)求数列{an}的通项公式;
(2)设${b_n}={a_{2n-1}}•{2^{a_n}}$,求数列{bn}的前n项和Tn.
分析 (1)运用数列的递推式:n=1时,a1=S1,当n≥2时,an=Sn-Sn-1,将n换为n-1,相减,再结合等差数列的定义和通项公式,即可得到所求;
(2)求得数列{bn}的通项,运用错位相减法,结合等比数列的求和公式,化简整理,即可得到所求和.
解答 解:(1)正项数列n的前n项和为Sn,且a1=1,an+12=Sn+1+Sn,①
当n≥2时,an2=Sn+Sn-1②
①-②可得an+12-an2=(an+1-an)(an+1+an)=an+1+an,
可得an+1-an=1,
则数列{an}是从第二项起,公差为1的等差数列,
a22=S2+S1=a1+a2+a1=2+a2,
解得a2=2(-1舍去),
当n≥2时,an=a2+(n-2)d=2+n-2=n;
上式对n=1也成立.
则数列{an}的通项公式an=n(n∈N*);
(2)由(1)得
${b_n}={a_{2n-1}}•{2^{a_n}}=({2n-1})•{2^n},{T_n}=2+3•{2^2}+5•{2^3}+…+({2n-1})•{2^n}$,③
$2{T_n}={2^2}+3•{2^3}+…+({2n-3})•{2^n}+({2n-1})•{2^{n+1}}$,④
③-④得,$-{T_n}=2+2×{2^2}+…+2×{2^n}-({2n-1})•{2^{n+1}}$,
所以$-{T_n}=2+\frac{{{2^3}•({1-{2^{n-1}}})}}{1-2}-({2n-1})•{2^{n+1}}$,
故${T_n}=({2n-3})•{2^{n+1}}+6$.
点评 本题考查数列的通项的求法,注意运用数列的递推式:n=1时,a1=S1,当n≥2时,an=Sn-Sn-1,考查数列的求和方法:错位相减法,同时考查等差数列的通项公式和等比数列的求和公式的运用,考查化简整理的运算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | {2} | B. | {3} | C. | {2,3,4} | D. | {1,2,3,4} |
| A. | a<$\frac{1}{3}$ | B. | $\frac{1}{3}$<a<$\frac{2}{3}$ | C. | a>1 | D. | $\frac{1}{3}$<a<$\frac{2}{3}$或a>1 |
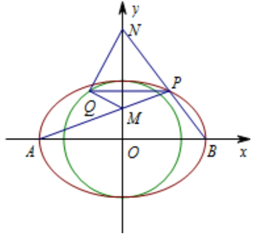 已知椭圆C:$\frac{x^2}{4}+\frac{y^2}{b^2}=1$(b>0),以椭圆C的短轴为直径的圆O经过椭圆C左右两个焦点,A,B是椭圆C的长轴端点.
已知椭圆C:$\frac{x^2}{4}+\frac{y^2}{b^2}=1$(b>0),以椭圆C的短轴为直径的圆O经过椭圆C左右两个焦点,A,B是椭圆C的长轴端点.