题目内容
19.设函数f(x)可导,则$\lim_{△x→0}\frac{{f(1)-f({1+△x})}}{3△x}$等于( )| A. | -f'(1) | B. | 3f'(1) | C. | $-\frac{1}{3}f'(1)$ | D. | $\frac{1}{3}f'(1)$ |
分析 将原式化简,利用导数的定义,即可求得答案.
解答 解:由$\lim_{△x→0}\frac{{f(1)-f({1+△x})}}{3△x}$=-$\frac{1}{3}$$\underset{lim}{△x→0}$$\frac{f(1+△x)-f(1)}{△x}$=-$\frac{1}{3}$f′(1),
∴$\lim_{△x→0}\frac{{f(1)-f({1+△x})}}{3△x}$=-$\frac{1}{3}$f′(1),
故选C.
点评 本题考查导数的定义,考查函数在某点处的导数,考查转化思想,属于基础题.

练习册系列答案
相关题目
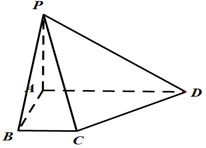 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,AD=3BC.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,AD=3BC.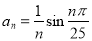 ,
,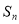 是
是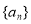 的前
的前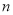 项和.在
项和.在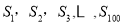 中,正数的个数是( )
中,正数的个数是( )