题目内容
7.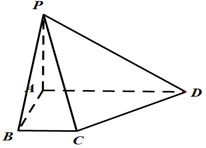 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,AD=3BC.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,AD=3BC.(I)求证:AB⊥PD;
(II)侧棱PA上是否存在点E,使得BE∥平面PCD?若存在,指出点E的位置并证明;若不存在,请说明理由.
分析 (I)欲证明AB⊥PD,只需推知AB与平面PD内的两条相交线垂直即可;
(II)在PA上存在三等分点E,使得AE=2EP,此时BE∥平面PCD.根据题意构建平行四边形BEFC,利用平行四边形的性质和直线与平面平行的判定定理进行证明即可.
解答 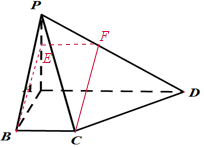 (I)证明:因为PA⊥平面ABCD,AB?平面ABCD,
(I)证明:因为PA⊥平面ABCD,AB?平面ABCD,
所以AB⊥PA,
因为底面ABCD为直角梯形,且AD∥BC,∠ABC=90°,
所以AB⊥AD.
又PA∩AD=A,所以AB⊥平面PAD,
又因为PD?平面PAD,所以AB⊥PD;
(II)解:在PA上存在三等分点E,使得AE=2EP,此时BE∥平面PCD.
证明如下:取PD上点F,使得DF=2FP,
连结BE,EF,FC,
则EF∥AD,且$EF=\frac{1}{3}AD$.
又AD=3BC,AD∥BC,
所以BC∥EF,且BC=EF,
因为四边形BEFC为平行四边形,
所以BE∥CF,
因为BE?平面PCD,CF?平面PCD,
所以BE∥平面PCD.
点评 本题考查线面垂直、线面平行的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
1.经过圆(x+1)2+(y-1)2=2的圆心C,且与直线x+y=0垂直的直线方程是( )
| A. | x+y+1=0 | B. | x+y-2=0 | C. | x-y+2=0 | D. | x-y-1=0 |
16.若θ是第二象限角,且$cos\frac{θ}{2}-sin\frac{θ}{2}=\sqrt{1-sinθ}$,则$\frac{θ}{2}$是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
19.设函数f(x)可导,则$\lim_{△x→0}\frac{{f(1)-f({1+△x})}}{3△x}$等于( )
| A. | -f'(1) | B. | 3f'(1) | C. | $-\frac{1}{3}f'(1)$ | D. | $\frac{1}{3}f'(1)$ |