题目内容
等比数列{an}的前n项和为Sn，a2=2a1，则
的值是 ．
| S4 |
| a4 |
考点：等比数列的性质
专题：等差数列与等比数列
分析：由题意可得公比q=2，由求和公式和通项公式可得S4和a4，代入计算可得．
解答：
解：由题意可得等比数列{an}的公比q=
=2，
∴S4=
=15a1，a4=a1•23=8a1，
∴
=
=
故答案为：
| a2 |
| a1 |
∴S4=
| a1(1-24) |
| 1-2 |
∴
| S4 |
| a4 |
| 15a1 |
| 8a1 |
| 15 |
| 8 |
故答案为：
| 15 |
| 8 |
点评：本题考查等比数列的性质，涉及通项公式和求和公式，属基础题．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
将函数y=
sin2x+cos2x-1的图象向右平移
个单位，所得函数图象的一个对称中心是（ ）
| 3 |
| π |
| 6 |
| A、（0，-1） | ||
B、（
| ||
C、（
| ||
D、（-
|
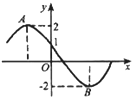如图所示为函数f（x）=2sin（ωx+φ）（ω＞0，| π |
| 2 |
| A、-1 | ||
B、-
| ||
C、
| ||
| D、1 |
设{an}是等差数列，从{a1，a2，a3，…，a20}中任取3个不同的数，使这三个数仍成等差数列，则这样不同的等差数列最多有（ ）
| A、90个 | B、120个 |
| C、160个 | D、180个 |
若函数y=x•2x 且y′=0，则x=（ ）
A、-
| ||
B、
| ||
| C、-ln2 | ||
| D、ln2 |