题目内容
设{an}是等差数列,从{a1,a2,a3,…,a20}中任取3个不同的数,使这三个数仍成等差数列,则这样不同的等差数列最多有( )
| A、90个 | B、120个 |
| C、160个 | D、180个 |
考点:等差关系的确定
专题:等差数列与等比数列
分析:当取连续的三项时,有{a1,a2,a3},{a2,a3,a4},…,{a18,a19,a20},共有18个,其倒序仍然成等差数列,因此共有36个;当取隔一项时,有{a1,a3,a5},{a2,a4,a6},…,{a16,a18,a20},共有16个,其倒序仍然成等差数列,因此共有32个;依此类推即可得出.
解答:
解:当取连续的三项时,有{a1,a2,a3},{a2,a3,a4},…,{a18,a19,a20},共有18个,其倒序仍然成等差数列,因此共有36个;
当取隔一项时,有{a1,a3,a5},{a2,a4,a6},…,{a16,a18,a20},共有16个,其倒序仍然成等差数列,因此共有32个;
…,
当取隔9项时,有{a1,a10,a19},{a2,a11,a20},共有2个,其倒序仍然成等差数列,因此共有4个.
综上可得:这样不同的等差数列最多有
=180.
故选:D.
当取隔一项时,有{a1,a3,a5},{a2,a4,a6},…,{a16,a18,a20},共有16个,其倒序仍然成等差数列,因此共有32个;
…,
当取隔9项时,有{a1,a10,a19},{a2,a11,a20},共有2个,其倒序仍然成等差数列,因此共有4个.
综上可得:这样不同的等差数列最多有
| 9×(36+4) |
| 2 |
故选:D.
点评:本题考查了等差数列的定义、分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
执行如图的程序框图,若输出的n=5,则输入整数p的最小值是( )


| A、6 | B、7 | C、8 | D、15 |
如图所示的程序框图表示求算式“2×4×8×16×32”的值,则判断框内可以填入( )
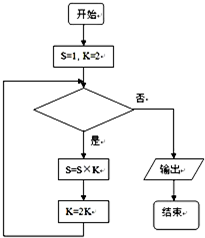

| A、k<10 | B、k<20 |
| C、k<30 | D、k<40 |
 在直角坐标系xOy中,单位圆O与x轴正半轴的交点为A,点P,Q在单位圆上,且满足
在直角坐标系xOy中,单位圆O与x轴正半轴的交点为A,点P,Q在单位圆上,且满足