根据下面程序框图.当n=2时.输出S=( )A．1000B．1950C．2850D．3800 题目和参考答案——青夏教育精英家教网—

题目内容

8．根据下面程序框图，当n=2时，输出S=（　　）

A．

1000

B．

1950

C．

2850

D．

3800

分析模拟执行程序，依次写出每次循环得到的S，i的值，当i=3时，满足条件i＞2，退出循环，输出S的值为2850．

解答解：模拟执行程序，可得
i=0，S=0
S=1000，i=1＜2；
S=1950，i=2；
S=2850，i=3＞2，
退出循环，输出S=2850．
故选：C．

点评算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视．程序填空也是重要的考试题型，这种题考试的重点有：①分支的条件②循环的条件③变量的赋值④变量的输出．其中前两点考试的概率更大．此种题型的易忽略点是：不能准确理解流程图的含义而导致错误．

练习册系列答案

19．若复数z满足（3-z）•i=2（i为虚数单位），则z=3+2i．

16．已知P是圆x²+y²=36的圆心，R是椭圆$\frac{x^2}{9}+\frac{y^2}{3}=1$上的一动点，且满足$\overrightarrow{PR}=3\overrightarrow{PQ}$．
（1）求动点Q的轨迹方程
（2）若直线y=x+1与曲线Q相交于A、B两点，求弦AB的长度．

3．

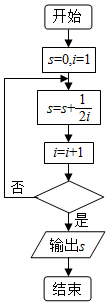如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{10}$的值的一个框图，其中菱形判断框内应填入的条件是（　　）

13．若运行如图所示程序框图，则输出结果S的值为（　　）

20．若（2x-1）²⁰¹⁶=a₀+a₁x+a₂x²+…+a₂₀₁₆x²⁰¹⁶，则$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{2016}}{{2}^{2016}}$=-1．

17．已知函数f（x）=a|x|-3a-1，若命题?x∈[-1，1]，使f（x）≠0是假命题，则实数a的取值范围为（　　）

A．

$（-∞，\;-\frac{1}{2}]$

B．

$（-∞，\;-\frac{1}{2}]∪（0，\;+∞）$

C．

$[-\frac{1}{2}，\;-\frac{1}{3}]$

D．

$（-∞，\;-\frac{1}{3}]∪$$[-\frac{1}{2}，\;0）$

18．函数y=（sinx-2）（cosx-2）的值域是（　　）

A．

[$\frac{9}{2}$-2$\sqrt{2}$，$\frac{9}{2}$+2$\sqrt{2}$]

B．

[$\frac{3}{2}$，$\frac{9}{2}$+2$\sqrt{2}$]

C．

[$\frac{3}{2}$，+∞）

D．

[$\frac{9}{2}$-2$\sqrt{2}$，$\sqrt{2}$]

试题分类