题目内容

9．设复数z满足z•（2+i）=10-5i（i为虚数单位），则z的共轭复数$\overline{z}$为（　　）
A．-3+4iB．-3-4iC．3+4iD．3-4i

分析 由z•（2+i）=10-5i，得z=$\frac{10-5i}{2+i}$，再由复数代数形式的乘除运算化简复数z，则z的共轭复数$\overline{z}$可求．

解答 解：由z•（2+i）=10-5i，
得$z=\frac{10-5i}{2+i}=\frac{（10-5i）（2-i）}{（2+i）（2-i）}=\frac{15-20i}{5}$=3-4i，
则z的共轭复数$\overline{z}$=3+4i．
故选：C．

点评 本题考查了复数代数形式的乘除运算，考查了共轭复数的求法，是基础题．

练习册系列答案
相关题目
19．若复数z满足（3-z）•i=2（i为虚数单位），则z=3+2i．
20．若（2x-1）2016=a0+a1x+a2x2+…+a2016x2016，则$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{2016}}{{2}^{2016}}$=-1．
17．已知函数f（x）=a|x|-3a-1，若命题?x∈[-1，1]，使f（x）≠0是假命题，则实数a的取值范围为（　　）
A．$（-∞，\;-\frac{1}{2}]$B．$（-∞，\;-\frac{1}{2}]∪（0，\;+∞）$C．$[-\frac{1}{2}，\;-\frac{1}{3}]$D．$（-∞，\;-\frac{1}{3}]∪$$[-\frac{1}{2}，\;0）$
4．已知向量$\overrightarrow m=（sinx，cosx），\overrightarrow n=（cosx，-\sqrt{3}cos（π+x））$（x∈R）函数f（x）=$\overrightarrow m•\overrightarrow n$
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）若函数y=f（x）的图象向右平移$\frac{π}{4}$个单位，再向上平移$\frac{\sqrt{3}}{2}$个单位，得到函数y=g（x）的图象，求y=g（x）在[0，$\frac{π}{4}$]上的最大值．
14．设椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），定义椭圆C的“相关圆”方程为x2+y2=$\frac{{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$．若抛物线y2=4x的焦点与椭圆C的一个焦点重合，且椭圆C短轴的一个端点和两个焦点构成直角三角形
（Ⅰ）求椭圆C的方程和“相关圆”E的方程；
（Ⅱ）过“相关圆”E上任意一点P的直线l：y=kx+m与椭圆交于A，B两点，O为坐标原点，若OA⊥OB，证明原点O到直线AB的距离为定值，并求m的取值范围．
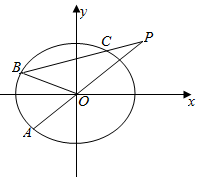1．如图，在平面直角坐标系xOy中，已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，A为椭圆上异于顶点的一点，点P满足$\overrightarrow{OP}$=2$\overrightarrow{AO}$．
（1）若点P的坐标为（2，$\sqrt{2}$），求椭圆的方程；
（2）设过点P的一条直线交椭圆于B，C两点，且$\overrightarrow{BP}$=m$\overrightarrow{BC}$，直线OA，OB的斜率之积为-$\frac{1}{2}$，求实数m的值．
18．函数y=（sinx-2）（cosx-2）的值域是（　　）
A．[$\frac{9}{2}$-2$\sqrt{2}$，$\frac{9}{2}$+2$\sqrt{2}$]B．[$\frac{3}{2}$，$\frac{9}{2}$+2$\sqrt{2}$]C．[$\frac{3}{2}$，+∞）D．[$\frac{9}{2}$-2$\sqrt{2}$，$\sqrt{2}$]
19．设各项为正数等比数列{an}的前n项和为Sn，已知S1=2，S3=14．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足bn=an•log2an，求{bn}的通项公式；
（3）求数列{bn}的前n项和Tn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网