在△ABC中.若A=30°.B=45°.$BC=\sqrt{6}$.则AC=$2\sqrt{3}$．题目和参考答案——青夏教育精英家教网—

题目内容

12．在△ABC中，若A=30°，B=45°，$BC=\sqrt{6}$，则AC=$2\sqrt{3}$．

分析利用正弦定理即可计算求解．

解答解：∵A=30°，B=45°，$BC=\sqrt{6}$，
∴由正弦定理$\frac{BC}{sinA}=\frac{AC}{sinB}$，可得：AC=$\frac{BCsinB}{sinA}$=$\frac{\sqrt{6}×\frac{\sqrt{2}}{2}}{\frac{1}{2}}$=2$\sqrt{3}$．
故答案为：2$\sqrt{3}$．

点评本题主要考查了正弦定理在解三角形中的应用，属于基础题．

练习册系列答案

3．

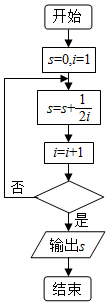如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{10}$的值的一个框图，其中菱形判断框内应填入的条件是（　　）

20．若（2x-1）²⁰¹⁶=a₀+a₁x+a₂x²+…+a₂₀₁₆x²⁰¹⁶，则$\frac{{a}_{1}}{2}$+$\frac{{a}_{2}}{{2}^{2}}$+…+$\frac{{a}_{2016}}{{2}^{2016}}$=-1．

7．若命题p：?x∈（0，+∞），x+$\frac{1}{2}$＞2，命题q：?x₀∈R，2 ^x0＜0，则下列为真命题的是（　　）

17．已知函数f（x）=a|x|-3a-1，若命题?x∈[-1，1]，使f（x）≠0是假命题，则实数a的取值范围为（　　）

A．

$（-∞，\;-\frac{1}{2}]$

B．

$（-∞，\;-\frac{1}{2}]∪（0，\;+∞）$

C．

$[-\frac{1}{2}，\;-\frac{1}{3}]$

D．

$（-∞，\;-\frac{1}{3}]∪$$[-\frac{1}{2}，\;0）$

4．已知向量$\overrightarrow m=（sinx，cosx），\overrightarrow n=（cosx，-\sqrt{3}cos（π+x））$（x∈R）函数f（x）=$\overrightarrow m•\overrightarrow n$
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）若函数y=f（x）的图象向右平移$\frac{π}{4}$个单位，再向上平移$\frac{\sqrt{3}}{2}$个单位，得到函数y=g（x）的图象，求y=g（x）在[0，$\frac{π}{4}$]上的最大值．

1．

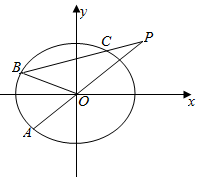如图，在平面直角坐标系xOy中，已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，A为椭圆上异于顶点的一点，点P满足$\overrightarrow{OP}$=2$\overrightarrow{AO}$．
（1）若点P的坐标为（2，$\sqrt{2}$），求椭圆的方程；
（2）设过点P的一条直线交椭圆于B，C两点，且$\overrightarrow{BP}$=m$\overrightarrow{BC}$，直线OA，OB的斜率之积为-$\frac{1}{2}$，求实数m的值．

2．已知α，β为锐角，且$\frac{sinβ}{sinα•cos（α+β）}$=λ，求证：tanβ=$\frac{λtanα}{1+（1+λ{）tan}^{2}α}$．

试题分类