题目内容
2.在△ABC中,a、b、c分别是角A、B、C的对边.求证:$\frac{cosB}{cosC}$=$\frac{c-bcosA}{b-ccosA}$.分析 将式子交叉相乘,利用两角和差的三角函数公式化简,逐步得出等价式,最后得出恒成立的式子即可.
解答 证明:$\frac{cosB}{cosC}$=$\frac{c-bcosA}{b-ccosA}$?bcosB-ccosAcosB=ccosC-bcosAcosC?b(cosB+cosAcosC)=c(cosC+cosAcosB)
?bsinAsinC=csinAsinB?abc=abc.
显然abc=abc恒成立.
∴$\frac{cosB}{cosC}$=$\frac{c-bcosA}{b-ccosA}$.
点评 本题考查了三角函数的恒等变换,属于中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
12.函数f(x)=sin(2x+φ)(|φ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{12}$个单位后的图象关于y轴对称,则函数f(x)在[0,$\frac{π}{4}$]上的最大值为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
10.在△ABC中,如果sinA:sinB:sinC=6:7:9,则△ABC一定是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 不能确定 |
17.已知$\vec a$=(-1,3),$\vec b$=(1,t),若($\vec a$-2$\vec b$)⊥$\vec a$,则|${\vec b}$|=( )
| A. | 5 | B. | $\sqrt{2}$ | C. | $\sqrt{10}$ | D. | $\sqrt{5}$ |
7.在数列{an}中,a1=1,且anan+1+$\sqrt{3}$(an-an+1)+1=0,则a2016=( )
| A. | 1 | B. | -1 | C. | 2+$\sqrt{3}$ | D. | 2-$\sqrt{3}$ |
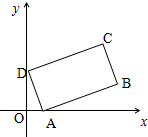 如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别位于x轴、y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}•\overrightarrow{OC}$的最大值是6.
如图,矩形ABCD中AD边的长为1,AB边的长为2,矩形ABCD位于第一象限,且顶点A,D分别位于x轴、y轴的正半轴上(含原点)滑动,则$\overrightarrow{OB}•\overrightarrow{OC}$的最大值是6. 如图,在平行四边形ABCD中,已知$\overrightarrow{|AB|}$=8,$\overrightarrow{|AD|}$=5,$\overrightarrow{CP}=3\overrightarrow{PD}$,$\overrightarrow{AP}•\overrightarrow{BP}=2$,则$\overrightarrow{AB}•\overrightarrow{AD}$=22.
如图,在平行四边形ABCD中,已知$\overrightarrow{|AB|}$=8,$\overrightarrow{|AD|}$=5,$\overrightarrow{CP}=3\overrightarrow{PD}$,$\overrightarrow{AP}•\overrightarrow{BP}=2$,则$\overrightarrow{AB}•\overrightarrow{AD}$=22.