题目内容
20.直线经过点(1,2),且与3x+2y-5=0垂直,则该直线方程为2x-3y+4=0.分析 用点斜式设出所求的直线,根据垂直关系求出直线的斜率,即可得出所求直线的方程.
解答 解:设所求的直线为y-2=k(x-1),
且该直线与直线3x+2y-5=0垂直,
所以k•(-$\frac{3}{2}$)=-1,解得k=$\frac{2}{3}$;
即所求直线的方程为y-2=$\frac{2}{3}$(x-1),
化为一般方程为2x-3y+4=0.
故答案为:2x-3y+4=0.
点评 本题考查了直线方程与垂直关系的应用问题,是基础题目.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
10.在△ABC中,如果sinA:sinB:sinC=6:7:9,则△ABC一定是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 不能确定 |
5.某校高三年级共有30个班,学校心理咨询室为了解同学们的心理状况,将每个班编号,依次为1到30,现用系统抽样方法,抽取6个班进行调查,若抽到的编号之和为87,则抽到的最小编号为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
20.某高中为了解全校学生每周参加体育运动的情况,随机从全校学生中抽取100名学生,统计他们每周参与体育运动的时间如下:
(1)作出样本的频率分布直方图;
(2)①估计该校学生每周参与体育运动的时间的中位数及平均数;
②若该校有学生3000人,根据以上抽样调查数据,估计该校学生每周参与体育运动的时间不低于8小时的人数.
| 每周参与运动的时间(单位:小时) | [0,4) | [4,8) | [8,12) | [12,16) | [16,20] |
| 频数 | 24 | 40 | 28 | 6 | 2 |
(2)①估计该校学生每周参与体育运动的时间的中位数及平均数;
②若该校有学生3000人,根据以上抽样调查数据,估计该校学生每周参与体育运动的时间不低于8小时的人数.
 如图,在平行四边形ABCD中,已知$\overrightarrow{|AB|}$=8,$\overrightarrow{|AD|}$=5,$\overrightarrow{CP}=3\overrightarrow{PD}$,$\overrightarrow{AP}•\overrightarrow{BP}=2$,则$\overrightarrow{AB}•\overrightarrow{AD}$=22.
如图,在平行四边形ABCD中,已知$\overrightarrow{|AB|}$=8,$\overrightarrow{|AD|}$=5,$\overrightarrow{CP}=3\overrightarrow{PD}$,$\overrightarrow{AP}•\overrightarrow{BP}=2$,则$\overrightarrow{AB}•\overrightarrow{AD}$=22.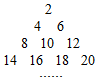 将正偶数排列如图,其中第i行和第j列的数表示为aij=(i,j∈N+),例如a43=18,若aij=2016,则i+j=63.
将正偶数排列如图,其中第i行和第j列的数表示为aij=(i,j∈N+),例如a43=18,若aij=2016,则i+j=63.