题目内容
对于任意实数x∈(-2,2],使(x2+x+1)a≤x3-1恒成立,则实数a的取值集合是 .
考点:函数恒成立问题
专题:函数的性质及应用
分析:先将原不等式化简,两边可以同时约分掉左边的因式,然后再转化为函数的最值问题来解.
解答:
解:因为x3-1=(x-1)(x2+x+1),且x2+x+1=(x+
)2+
>0恒成立.
故原不等式可化为a≤x-1,x∈(-2,2]恒成立.
只需a≤(x-1)min即可,因为y=x-1是增函数,所以只需a≤-2-1=-3即可.
故a的取值集合为{a|a≤-3}.
故答案为{a|a≤-3}.
| 1 |
| 2 |
| 3 |
| 4 |
故原不等式可化为a≤x-1,x∈(-2,2]恒成立.
只需a≤(x-1)min即可,因为y=x-1是增函数,所以只需a≤-2-1=-3即可.
故a的取值集合为{a|a≤-3}.
故答案为{a|a≤-3}.
点评:本题考查了不等式恒成立问题的解题思路.一般转化为函数的最值问题来解.

练习册系列答案
相关题目
如表是函数u,v随自变量x变化的一组数据,由此判断u,v最符合的函数模型分别是( )
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| U | 0.0631 | 0.26 | 1.11 | 3.96 | 16.05 | 63.98 |
| v | 11.92 | 14.95 | 18.01 | 21.03 | 24.11 | 26.95 |
| A、二次函数型和一次函数型 |
| B、指数函数型和一次函数型 |
| C、二次函数型和对数函数型 |
| D、指数函数型和对数函数型 |
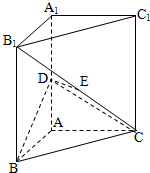 如图,直三棱柱ABC-A1B1C1,AB=AC=1,AA1=2.AB⊥AC.
如图,直三棱柱ABC-A1B1C1,AB=AC=1,AA1=2.AB⊥AC.