题目内容

函数y=cos2x+2sinxcosx的最小正周期T=
 
．
考点：二倍角的正弦,三角函数的周期性及其求法
专题：三角函数的求值,三角函数的图像与性质
分析：利用二倍角公式以及两角和与差的三角函数化简函数的表达式，然后求出函数的周期．
解答： 解：函数y=cos2x+2sinxcosx
=
2
sin（2x+
π
4
）．
所以函数的最小正周期T=
2π
2
=π．
故答案为：π．
点评：本题考查三角函数的周期的求法，两角和与差的三角函数以及二倍角公式的应用．
练习册系列答案
相关题目
某班主任对全班50名学生进行了作业量多少的调查，喜欢玩脑游戏的同学认为作业多的有15人，认为作业不多的有5人，不喜欢玩电脑游戏的同学认为作业多的有10人，认为作业不多的有20人，
（1）根据以上数据建立一个2×2的列联表；
（2）在犯错误的概率不超过多少的前提下认为玩电脑游戏与作业量的多少有关系？
对于定义在区间[a，b]上的函数f（x），给出下列命题：
（1）若f（x）在多处取得极大值，那么f（x）的最大值一定是所有极大值中最大的一个值；
（2）若函数f（x）的极大值为m，极小值为n，那么m＞n；
（3）若x0∈（a，b），在x0左侧附近f′（x）＜0，且f′（x0）=0，则x0是f（x）的极大值点；
（4）若f′（x）在[a，b]上恒为正，则f（x）在[a，b]上为增函数，
其中正确命题的序号是
 
．
小明晚上放学回家要做如下事情：复习功课用30分钟，休息用30分钟，烧水用15分钟，做作业用25分钟，要完成这些事情，小明要花费的最少时间为
 
分钟．
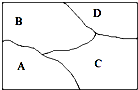如图，要给地图A、B、C、D四个区域分别涂上红、黄、蓝3种颜色中的某一种，允许同一种颜色使用多次，但相邻区域必须涂不同的颜色，不同的涂色方案有
 
种．
设i为虚数单位，若复数（m+1）+（m2-1）i为实数，则m的值为
 
．
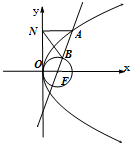如图，抛物线C：y2=2px（p＞0）的焦点为F，A为C上的点，以F为圆心，
P
2
为半径的圆与线段AF的交点为B，∠AFx=60°，A在y轴上的射影为N，则∠ONB=
 
．
函数f（x）=（m2-m-1）x1-2m是幂函数，且在x∈（0，+∞）上是增函数，则实数m=
 
．
设直线l经过点M（1，5）、倾斜角为
π
3
，则直线l的参数方程可为（　　）
A、
x=1-
1
2
t
y=5+
3
2
t
B、
x=1+
3
2
t
y=5+
1
2
t
C、
x=1+
1
2
t
y=5+
3
2
t
D、
x=-1+
1
2
t
y=-5+
3
2
t

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网