题目内容
6．已知函数f（x）=ax3-5x2-bx，a，b∈R，x=3是f（x）的极值点，且f（1）=-1．（1）求实数a，b的值；
（2）求f（x）在[2，4]上的最小值和最大值．
分析 （1）求出函数的导数，计算f（1），f′（3），求出a，b的值即可；
（2）求出函数的导数，解关于导函数的不等式，求出函数的单调区间，从而求出函数的最大值和最小值即可．
解答 解：（1）f′（x）=3ax2-10x-b，
f′（3）=0，即27a-30-b=0，
又f（1）=-1，
故a=1，b=-3；
（2）由（1）f（x）=x3-5x2+3x，
f′（x）=3x2-10x+3，
令f′（x）＞0，解得：3＜x＜4，
令f′（x）＜0，解得：2＜x＜3，
故f（x）在（2，3）递减，在（3，4）递增，
故f（x）min=f（3）=-9，f（x）max=f（4）=-4．
点评 本题考查了函数的单调性、最值问题，考查导数的应用，是一道中档题．
练习册系列答案
相关题目
17．某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制，已知所有这些学生的原始成绩均分布在[50，100]内，发布成绩使用等级制各等级划分标准见下表，规定：A、B、C三级为合格等级，D为不合格等级．
为了解该校高一年级学生身体素质情况，从中抽取了n名学生的原始成绩作为样本进行统计，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图如图1所示，样本中分数在80分及以上的所有数据的茎叶图如图2所示．
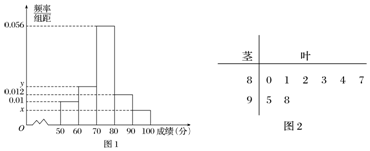
（1）求n和频率分布直方图中x，y的值；
（2）根据样本估计总体的思想，以事件发生的频率作为相应事件发生的概率，若在该校高一学生中任选3人，求至少有1人成绩是合格等级的概率．
| 百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
| 等级 | A | B | C | D |
（1）求n和频率分布直方图中x，y的值；
（2）根据样本估计总体的思想，以事件发生的频率作为相应事件发生的概率，若在该校高一学生中任选3人，求至少有1人成绩是合格等级的概率．
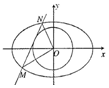如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，短轴长为2，直线l与圆O：x2+y2=$\frac{4}{5}$相切，且与椭圆C相交于M、N两点．
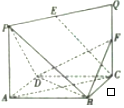如图，ACQP所在的平面与菱形ABCD所在的平面相互垂直，交线为AC，若$AC=\sqrt{2}AP，E，F$分别是PQ，CQ的中点．求证：