题目内容
(本小题13分)已知A为椭圆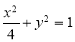 上的点,过A作AB
上的点,过A作AB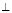 x轴,垂足为B,延长BA到C使得
x轴,垂足为B,延长BA到C使得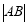 =
=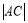 。
。
(1) 求点C的轨迹方程;
(2)直线l过点D (2,3)且与点C的轨迹只有一个交点,求l 的方程。
(1) ;(2) 5x-12y+26=0或x=2
;(2) 5x-12y+26=0或x=2
【解析】
试题分析:(1)设C(x,y),A ,则B
,则B ,因为
,因为 ,所以A是BC的中点,
,所以A是BC的中点,
所以 ,因为点A在椭圆
,因为点A在椭圆 ,即
,即 ,把点A坐标代入可得
,把点A坐标代入可得 ,
,
所以点C的轨迹方程为
(2)因为直线l与 只有一个交点,所以直线l与圆只有一个交点相切,
只有一个交点,所以直线l与圆只有一个交点相切,
当直线l的斜率存在时,设直线l的方程为y-3=k(x-2),即kx-y+3-2k=0
由 ,解得
,解得 ,所以直线l的方程为5x-12y+26=0
,所以直线l的方程为5x-12y+26=0
当直线l的斜率不存在,即方程为x=2,也满足
所以直线l的方程为5x-12y+26=0或x=2
考点:考查了求动点的轨迹方程,直线与圆的位置关系
点评:利用代入法(相关点法)求轨迹方程,注意分类讨论直线方程

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,焦点坐标为
,焦点坐标为 和
和 的双曲线
的双曲线 ,准线方程为
,准线方程为 的椭圆
的椭圆 轴的正半轴上,焦点到准线的距离为4的抛物线
轴的正半轴上,焦点到准线的距离为4的抛物线 满足约束条件
满足约束条件 ,则
,则 的最小值为( )
的最小值为( ) B.
B. C.
C.  D.
D. 
 是定义域为R的奇函数,且当
是定义域为R的奇函数,且当 时,
时, .则函数
.则函数 的零点的个数为( )
的零点的个数为( ) ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
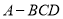 中,
中,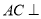 底面
底面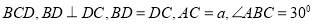 ,则点
,则点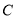 到平面
到平面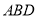 的距离是_____________。
的距离是_____________。  与圆
与圆 交于
交于 两点,则
两点,则 (
( 为原点)的面积为( )
为原点)的面积为( ) B.
B. C.
C. D.
D.
 ,则关于
,则关于 的不等式
的不等式 的解集是( )
的解集是( ) B.
B. C.
C. D.
D.
 中,
中, ,
, .
. 求角
求角 的值;
的值; 设
设 ,求
,求 .
.