题目内容
(12分)分别求适合下列条件的圆锥曲线的标准方程:
(1)离心率为 ,焦点坐标为
,焦点坐标为 和
和 的双曲线
的双曲线
(2)离心率 ,准线方程为
,准线方程为 的椭圆
的椭圆
(3)焦点在 轴的正半轴上,焦点到准线的距离为4的抛物线
轴的正半轴上,焦点到准线的距离为4的抛物线
(1) ;(2)
;(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)由焦点坐标可得 的值,由离心率可得
的值,由离心率可得 的值,根据公式
的值,根据公式 可得
可得 .从而可求得双曲线方程. (2)由准线方程可知椭圆焦点在
.从而可求得双曲线方程. (2)由准线方程可知椭圆焦点在 轴上,根据离心率,和准线可解得
轴上,根据离心率,和准线可解得 与
与 的值.根据公式
的值.根据公式 可得
可得 .从而可得椭圆方程. (3)由已知可设抛物线方程为方程为
.从而可得椭圆方程. (3)由已知可设抛物线方程为方程为 ,由已知可得
,由已知可得 ,从而可得抛物线方程.
,从而可得抛物线方程.
试题解析:(1)设双曲线标准方程为
由已知得:
 ,所以
,所以 ,故
,故 ..3分
..3分
所以双曲线的方程为: .4分
.4分
(2)由已知可设椭圆的标准方程为
有条件得: ,解得
,解得 ,
, .6分
.6分
所以 ,所以椭圆的方程为:
,所以椭圆的方程为: 8分
8分
(3)当抛物线的焦点在 轴的正半轴上,可设方程为
轴的正半轴上,可设方程为
由条件得 ,所以抛物线的方程为
,所以抛物线的方程为 .12分
.12分
考点:圆锥曲线的标准方程,简单几何性质.

练习册系列答案
相关题目
 的值域是( )
的值域是( )  B.
B. C.
C.  D.
D. 

 B.
B. C.
C. D.3
D.3 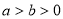 ,椭圆
,椭圆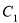 的方程为
的方程为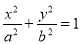 ,双曲线
,双曲线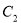 的方程为
的方程为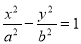 ,
,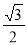 ,则
,则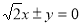 B.
B.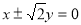 C.
C.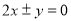 D.
D.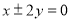
 ,
, ”的否定是
”的否定是 ,
,
 D.
D.
 则
则 ”的逆否命题是____________
”的逆否命题是____________ 的焦点坐标( )
的焦点坐标( ) B.
B. C.
C. D.
D.

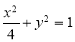 上的点,过A作AB
上的点,过A作AB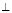 x轴,垂足为B,延长BA到C使得
x轴,垂足为B,延长BA到C使得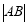 =
=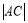 。
。