题目内容
在三棱锥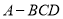 中,
中,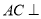 底面
底面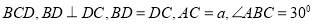 ,则点
,则点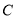 到平面
到平面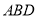 的距离是_____________。
的距离是_____________。

【解析】
试题分析:∵AC⊥平面BCD,BC、BD 平面BCD,∴AC⊥BC,BD⊥AC,
平面BCD,∴AC⊥BC,BD⊥AC,
∵BD⊥DC,AC∩CD=D,∴BD⊥平面ACD,
∵AD 平面ACD,∴BD⊥AD,∴△ABD是直角三角形,
平面ACD,∴BD⊥AD,∴△ABD是直角三角形,
∵AC=a,∠ABC=30°,∴AB=2AC=2a,BC= a,
a,
∵△DBC是等腰直角三角形,
∴ ,
,
∴ ,
,
∵ ,
,
∴ ,
,
设C到平面ABD距离为d,
由 ,可得
,可得 ,∴
,∴ .
.
考点:考查了点到平面的距离
点评:点到平面的距离可以用等体积法求,也可以过点C作CE⊥AD于点E,证明CE是点C到平面ABD的距离

练习册系列答案
相关题目
 则
则 ”的逆否命题是____________
”的逆否命题是____________ ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式 对定义域中的每一个
对定义域中的每一个 都成立,则称函数
都成立,则称函数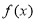 是“(
是“(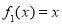 是否为 “(
是否为 “( 是“(
是“( ;
;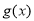 是“(
是“( 时,
时,

 ,若当
,若当 时,都有
时,都有 ,试求
,试求 的取值范围.
的取值范围. 的值域为( )
的值域为( ) B.
B. C.
C. D.
D.
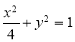 上的点,过A作AB
上的点,过A作AB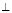 x轴,垂足为B,延长BA到C使得
x轴,垂足为B,延长BA到C使得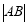 =
=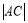 。
。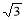 ,CC1=
,CC1=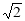 ,则二面角C1—BD—C的大小为( )
,则二面角C1—BD—C的大小为( )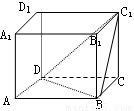
 ”的逆命题;
”的逆命题; ”;
”;
 ,
, ≥0”的否定是命题q:“
≥0”的否定是命题q:“
 ,
, ”,且命题q为假命题.
”,且命题q为假命题. ,
, ,
, ,则( )
,则( ) B.
B. C.
C. D.
D.
 的前
的前 项和为
项和为 ,且
,且 ,
, 为等差数列,则
为等差数列,则 ( )
( ) B.
B. C.
C. D.
D.