题目内容
(本小题满分12分)在 中,
中, ,
, .
.
 求角
求角 的值;
的值;
 设
设 ,求
,求 .
.
(1)  ;(2)
;(2)  .
.
【解析】
试题分析:(1)利用三角形内角和定理可得: ,结合两角和的正切公式得:
,结合两角和的正切公式得: 由已知
由已知 代入可求出
代入可求出 ,进而求出
,进而求出 ;(2)根据题意和(1)中所求
;(2)根据题意和(1)中所求 ,这样三角形的三个角均已知或求出,题(2)还有一个小条件:
,这样三角形的三个角均已知或求出,题(2)还有一个小条件: ,很显然想到运用正弦定理进行解题,又因为
,很显然想到运用正弦定理进行解题,又因为 ,由同角三角函数关系可得:
,由同角三角函数关系可得: ,而
,而 ,且
,且 为锐角,可求得
为锐角,可求得 . 所以在△
. 所以在△ 中,由正弦定理得,
中,由正弦定理得, .
.
试题解析:(1)  (3分)
(3分)
 (6分)
(6分)
(2)因为
 ,
,
而 ,且
,且 为锐角,可求得
为锐角,可求得 . (9分)
. (9分)
所以在△ 中,由正弦定理得,
中,由正弦定理得, . (12分)
. (12分)
考点:1.两角和的正切公式;2.同角三角函数的应用;3.正弦定理的应用

练习册系列答案
相关题目
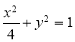 上的点,过A作AB
上的点,过A作AB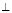 x轴,垂足为B,延长BA到C使得
x轴,垂足为B,延长BA到C使得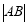 =
=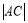 。
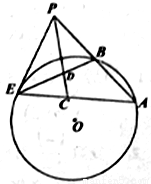
。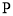 作圆
作圆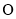 的割线
的割线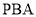 与切线
与切线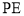 ,
,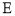 为切点,连接
为切点,连接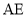 ,
,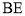 ,
,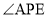 的平分线与
的平分线与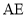 ,
,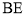 分别交于点
分别交于点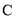 ,
,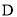 ,其中
,其中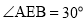 .
.
 求证:
求证: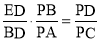 ;
;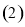 求
求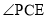 的大小.
的大小. ,
, 满足约束条件
满足约束条件 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 作圆
作圆 的割线
的割线 与切线
与切线 ,
, 为切点,连接
为切点,连接 ,
, ,
, 的平分线与
的平分线与 ,
, 分别交于点
分别交于点 ,
, ,其中
,其中 .
.
 求证:
求证: ;
; 求
求 的大小.
的大小. 的前
的前 项和为
项和为 ,且
,且 ,
, 为等差数列,则
为等差数列,则 ( )
( ) B.
B. C.
C. D.
D.
 ,
, 满足约束条件
满足约束条件 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
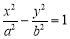 (a>0,b>0)的左、右焦点,点F1关于渐近线的对称点恰好落在以F2为圆心,|OF2|为半径的圆上,则该双曲线的离心率为 ( )
(a>0,b>0)的左、右焦点,点F1关于渐近线的对称点恰好落在以F2为圆心,|OF2|为半径的圆上,则该双曲线的离心率为 ( )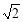 (B)
(B)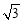
 ___________.
___________.