题目内容
已知函数f（x）=ax3-3x2+1，若f（x）存在唯一的零点x0，且x0＜0，则a的取值范围是（ ）
| A、（2，+∞） |
| B、（1，+∞） |
| C、（-∞，-2） |
| D、（-∞，-1） |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：由题意判断出a＞0，再由题意可知f（
）＞0，从而求出a
| 2 |
| a |
解答：
解：∵函数f（x）=ax3-3x2+1，f（0）=1，且f（x）存在唯一的零点x°，且x°＜0，
∴a＞0，
∴f′（x）=3ax2-6x=3x（ax-2）=0时的解为x=0，x=
；
∴f（
）=a（
）3-3（
）2+1=
＞0，
则a＞2．
故选：A
∴a＞0，
∴f′（x）=3ax2-6x=3x（ax-2）=0时的解为x=0，x=
| 2 |
| a |
∴f（
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| a2-4 |
| a2 |
则a＞2．
故选：A
点评：本题考查了函数的零点的判断，求导数判断求解即可，
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
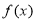是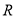
上的增函数，
，
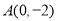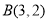是其图象上的两点，那么
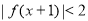的解集是 （ ）
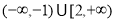
，则输出的结果是 ．
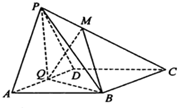如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点，PA=PD=AD=2．
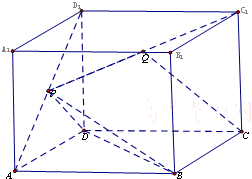如图，在正方体ABCD-A1B1C1D1中，P为线段AD1上的中点，Q为线段PC1上的中点．已知平面向量
，
，|
|=2，
=（2，
），若|
-
|=
，则
•
的值是（ ）
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| 6 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f（x）=x3-3x+m恰有2个不同的零点，则实数m的值为（ ）
| A、±2 | B、±1 |
| C、-2或1 | D、-1或2 |