��Ŀ����
18��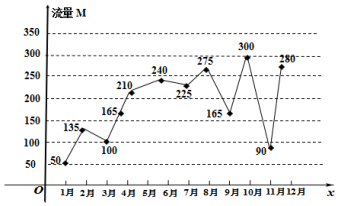 ij�˵��ֻ�ʹ�õ���ÿ��300M�����ײͣ���ͼ��¼��ij����ȥ��1�µ�12�µ�����ʹ����������к�������·ݣ��������������
ij�˵��ֻ�ʹ�õ���ÿ��300M�����ײͣ���ͼ��¼��ij����ȥ��1�µ�12�µ�����ʹ����������к�������·ݣ����������������������һ�������ȡһ���µ�����ʹ���������ʹ����������180M�ĸ��ʣ�
����������12���������ѡ�������������½��й۲죬�� ��ѡ�����µ�����ʹ������У��м��µ�����ʹ��������������µĸ��ʣ�
���� ������ͼ�жϴ��ĸ��¿�ʼ�������ĸ��µ�����ʹ�õ��������������۲�Ҫ��֤����
���� ��������������150MΪ�¼�A����һ�깲��12���£�����1�£�2�£�3�£�4�£�9��11�¹�6������������180M���ɴ������ʹ����������180M�ĸ��ʣ�
��������ѡ�����µ�����ʹ������У��м��µ�����ʹ���������������Ϊ�¼�B�������оٷ��������һ�������ȡ���������µ�ʹ�������IJ�ͬȡ������ѡ�����µ�����ʹ������У��м��µ�����ʹ��������������µ�����������ɴ�����������
����9�£�10�£�11�£�12�����ĸ��µ�����ʹ������������
��� ����С�13�֣�
�⣺��������������150MΪ�¼�A����һ�깲��12���£�
����1�£�2�£�3�£�4�£�9��11�¹�6������������180M������2�֣�
����$P��A��=\frac{6}{12}=\frac{1}{2}$������4�֣�
��������ѡ�����µ�����ʹ������У�
�м��µ�����ʹ���������������Ϊ�¼�B��
����һ�������ȡ���������µ�ʹ��������
��1��2��3 ������2��3��4 ������3��4��5 ����
��4��5��6 ������5��6��7 ������6��7��8 ����
��7��8��9 ������8��9��10 ������9��10��11 ����
��10��11��12 ������10��ȡ��������6�֣�
���У�2��3��4 ������6��7��8 ������8��9��10 ������10��11��12 ��4�������������������8�֣�
����$P��B��=\frac{4}{10}=\frac{2}{5}$������10�֣�
����9�£�10�£�11�£�12�����ĸ��µ�����ʹ��������������13�֣�
���� ���⿼����ʵ������鷽��ļ��㣬�ǻ����⣬����ʱҪ�������⣬ע���оٷ��ĺ������ã�

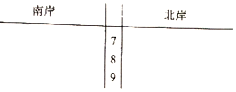 Ϊ����Ӧ���С������˾Ӹ۳ǣ��������������ij�������ſ�չ�ԡ��ذ�ľ��Ϫ������ĸ�ӡ�Ϊ����Ļ������������ľ��Ϫ�����Ӷηֳ�10�Σ�����֯����ɲ�ְ����ÿһ�ε��ϡ����������л����ۺϲ������õ���ֵ���������
Ϊ����Ӧ���С������˾Ӹ۳ǣ��������������ij�������ſ�չ�ԡ��ذ�ľ��Ϫ������ĸ�ӡ�Ϊ����Ļ������������ľ��Ϫ�����Ӷηֳ�10�Σ�����֯����ɲ�ְ����ÿһ�ε��ϡ����������л����ۺϲ������õ���ֵ���������| �ϰ� | 77 | 92 | 84 | 86 | 74 | 76 | 81 | 71 | 85 | 87 |
| ���� | 72 | 87 | 78 | 83 | 83 | 85 | 75 | 89 | 90 | 95 |
��2�����ݱ��е�������ɾ�Ҷͼ��
��3���ֱ����������ֵ����λ�������������ǵ�ƽ�������ԴӼ�����������������������ı߱������ã�
| A�� | f��x��=x3 | B�� | f��x��=x${\;}^{\frac{1}{2}}$ | C�� | f��x��=3x | D�� | f��x��=��$\frac{1}{2}$��x |
| A�� | [ln2��ln$\frac{3}{2}$+$\frac{1}{3}$] | B�� | ��ln2��ln$\frac{3}{2}$+$\frac{1}{3}$�� | C�� | ��$\frac{2}{3}$��ln2] | D�� | ��$\frac{2}{3}$��ln$\frac{3}{2}$+$\frac{1}{3}$] |
| A�� | 0.6 | B�� | 0.4 | C�� | 0.3 | D�� | 0.2 |