题目内容
9.下列函数中,满足“f(x+y)=f(x)f(y)”的单调递增函数是( )| A. | f(x)=x3 | B. | f(x)=x${\;}^{\frac{1}{2}}$ | C. | f(x)=3x | D. | f(x)=($\frac{1}{2}$)x |
分析 可先设f(x)为指数函数,并给出证明,再根据指数函数单调性的要求,得出C选项符合题意.
解答 解:指数函数满足条件“f(x+y)=f(x)f(y)”,验证如下:
设f(x)=ax,则f(x+y)=ax+y,
而f(x)f(y)=ax•ay=ax+y,
所以,f(x+y)=f(x)f(y),
再根据题意,要使f(x)单调递增,只需满足a>1即可,
参考各选项可知,f(x)=3x,即为指数函数,又为增函数,
故选:C.
点评 本题主要考查了指数函数的图象与性质,以及同底指数幂的运算性质,属于基础题.

练习册系列答案
相关题目
19.已知a>0,函数f(x)=ax2+bx+c,若x0满足2ax0+b=0,则下列选项中是假命题的是( )
| A. | ?x∈R,f(x)≤f(x0) | B. | ?x∈R,f(x)≥f(x0) | C. | ?x∈R,f(x)≤f(x0) | D. | ?x∈R,f(x)≥f(x0) |
17.“双曲线渐近线方程为y=±2x”是“双曲线方程为x2-$\frac{{y}^{2}}{4}$=λ(λ为常数且λ≠0)”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.函数f(x)=x2-4x+3的最小值是( )
| A. | 3 | B. | 0 | C. | -1 | D. | -2 |
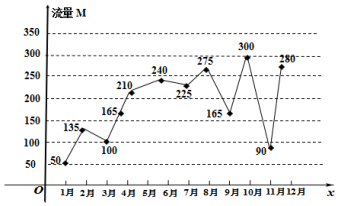 某人的手机使用的是每月300M流量套餐,如图记录了某人在去年1月到12月的流量使用情况.其中横轴代表月份,纵轴代表流量.
某人的手机使用的是每月300M流量套餐,如图记录了某人在去年1月到12月的流量使用情况.其中横轴代表月份,纵轴代表流量.