题目内容
7．
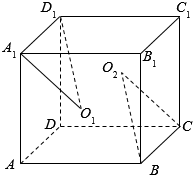如图，在正方体ABCD-A1B1C1D1，O1，O2分别是正方形ABB1A1、DCC1D1的对角线的交点，求证：∠A1O1D1=∠CO2B．
分析 根据题意，连接BO1，D1O2，证明四边形BCD1A1和四边形BO1D1O2是平行四边形；由此得出∠BO1D1=∠BO2D1，∠A1O1D1=∠CO2B．
解答 
解：连接BO1，D1O2，如图所示；
则BC∥AD，且BC=AD，AD∥A1D1，且AD=A1D1，
∴BC∥A1D1，且BC=A1D1，
∴四边形BCD1A1是平行四边形，
同理，四边形BO1D1O2是平行四边形；
∴∠BO1D1=∠BO2D1，
∴180°-∠BO1D1=180°-∠BO2D1，
即∠A1O1D1=∠CO2B．
点评 本题考查了空间中的平行关系的应用问题，也考查了逻辑推理与空间想象能力，是基础题目．
练习册系列答案
相关题目
17．已知平面α与平面β交于直线l，且直线a?α，直线b?β，则下列命题错误的是（ ）
| A． | 若α⊥β，a⊥b，且b与l不垂直，则a⊥l | B． | 若α⊥β，b⊥l，则a⊥b | ||
| C． | 若a⊥b，b⊥l，且a与l不平行，则α⊥β | D． | 若a⊥l，b⊥l，则α⊥β |
12．若关于x的不等式ex（ax+1）≥a2ex2+aex（a∈R）在（0，+∞）上恒成立，则a的最大值为（ ）
| A． | -$\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
17．设P是不等式组$\left\{\begin{array}{l}{x-2y+2≤0}\\{x+y-1≥0}\\{y≤2}\end{array}\right.$表示的平面区域内的一点，点Q（-3，0），则|PQ|的最大值为（ ）
| A． | $\sqrt{29}$ | B． | $\sqrt{31}$ | C． | $\sqrt{10}$ | D． | 4 |