题目内容
15.为迎接2016年春节的到来,某公司制作了猴年吉祥物,该吉祥物每个成本为6元,每个售价为x(6<x<11)元,预计该产品年销售量为m万个,已知m与售价x的关系满足:m=68-k(x-5)2+x,且当售价为10元时,年销售量为28万个.(1)求该吉祥物年销售利润y关于售价x的函数关系式;
(2)求售价为多少时,该吉祥物的年利润最大,并求出最大年利润.
分析 (1)易知68-k(10-5)2+10=28,从而解得k=2;从而化简y=-2x3+33x2-108x-108(6<x<11);
(2)求导y′=-6(x-2)(x-9),从而判断函数的单调性,从而求最值.
解答 解:(1)∵m=68-k(x-5)2+x,
∴68-k(10-5)2+10=28,
解得,k=2;
∴m=68-2(x-5)2+x=-2x2+21x+18.
∴y=m(x-6)=(-2x2+21x+18)(x-6)
=-2x3+33x2-108x-108(6<x<11),
(2)由(1)知,y′=-6x2+66x-108=-6(x-2)(x-9),
令y′>0解得,6<x<9;令y′<0解得,9<x<11;
故y=-2x3+33x2-108x-108在(6,9)上单调递增,在(9,11)上单调递减;
故x=9时,年利润最大,最大为135万元.
答:售价为9元时,该吉祥物年利润最大,且最大年利润为135万元.
点评 本题考查了导数的综合应用及导数在实际问题中的应用.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
5.已知集合M={0,1,2,3,4},N={x|1<log2(x+2)<2},则M∩N=( )
| A. | {1} | B. | {2,3} | C. | {0,1} | D. | {2,3,4} |
6.某公司从代理的A,B,C,D四种产品中,按分层抽样的方法抽取容量为110的样本,已知A,B,C,D四种产品的数量比是2:3:2,:4,则该样本中D类产品的数量为( )
| A. | 22 | B. | 33 | C. | 44 | D. | 55 |
10.已知函数f(x)=2x2+ax-2b,若a,b都是区间[0,4]内的数,则使f(1)<0的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{8}$ |

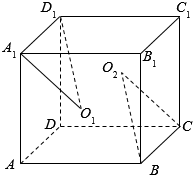 如图,在正方体ABCD-A1B1C1D1,O1,O2分别是正方形ABB1A1、DCC1D1的对角线的交点,求证:∠A1O1D1=∠CO2B.
如图,在正方体ABCD-A1B1C1D1,O1,O2分别是正方形ABB1A1、DCC1D1的对角线的交点,求证:∠A1O1D1=∠CO2B.