题目内容
12.若关于x的不等式ex(ax+1)≥a2ex2+aex(a∈R)在(0,+∞)上恒成立,则a的最大值为( )| A. | -$\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
分析 由题意可得ex(ax+1)≥aex(ax+1),即有(ax+1)(ex-aex)≥0,由不等式在(0,+∞)上恒成立,可得a>0,且ae≤$\frac{{e}^{x}}{x}$的最小值,运用导数求得右边函数的单调区间和最小值,即可得到所求a的最大值.
解答 解:关于x的不等式ex(ax+1)≥a2ex2+aex,
即为ex(ax+1)≥aex(ax+1),
即有(ax+1)(ex-aex)≥0,
由不等式在(0,+∞)上恒成立,
可得a>0,且ae≤$\frac{{e}^{x}}{x}$的最小值,
由f(x)=$\frac{{e}^{x}}{x}$的导数为$\frac{{e}^{x}(x-1)}{{x}^{2}}$,
当x>1时,f′(x)>0,f(x)递增;
当0<x<1时,f′(x)<0,f(x)递减.
可得x=1处,f(x)取得最小值,且为e,
则ae≤e,可得0<a≤1,
故a的最大值为1.
故选:C.
点评 本题考查不等式恒成立问题的解法,注意运用分解因式和参数分离,转化为求函数的最值求法,考查导数的运用:求最值,考查运算能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目

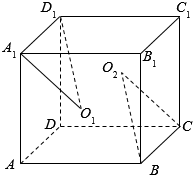 如图,在正方体ABCD-A1B1C1D1,O1,O2分别是正方形ABB1A1、DCC1D1的对角线的交点,求证:∠A1O1D1=∠CO2B.
如图,在正方体ABCD-A1B1C1D1,O1,O2分别是正方形ABB1A1、DCC1D1的对角线的交点,求证:∠A1O1D1=∠CO2B.