题目内容
17.设P是不等式组$\left\{\begin{array}{l}{x-2y+2≤0}\\{x+y-1≥0}\\{y≤2}\end{array}\right.$表示的平面区域内的一点,点Q(-3,0),则|PQ|的最大值为( )| A. | $\sqrt{29}$ | B. | $\sqrt{31}$ | C. | $\sqrt{10}$ | D. | 4 |
分析 作出平面区域,观察图形得出最有解得位置.
解答  解:作出平面区域如图:
解:作出平面区域如图:
由图形可知当Q为直线x-2y+2=0与y=2的交点时,|PQ|最大.
解方程组$\left\{\begin{array}{l}{y=2}\\{x-2y+2=0}\end{array}\right.$得x=2,y=2.
∴|PQ|的最大值为$\sqrt{(2+3)^{2}+(2-0)^{2}}$=$\sqrt{29}$.
故选A.
点评 本题考查了简单的线性规划,作出平面区域是解题关键,属于基础题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
8.已知数列{an}中,a1=1,$\frac{1}{{a}_{n+1}}$=$\frac{1}{{a}_{n}}$+$\frac{1}{3}$,则a10等于( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | 以上都不对 |
12.cos$\frac{3π}{4}$等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
9.将8分为两个非负数之和,使其立方之和为最小,则分法为( )
| A. | 2和6 | B. | 4和4 | C. | 3和5 | D. | 以上都不对 |
9.在平面xOy内,向图形x2+y2≤4内投点,则点落在由不等式组$\left\{\begin{array}{l}x-y≥0\\ x+y≥0\end{array}\right.$所确定的平面区域的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
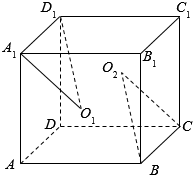 如图,在正方体ABCD-A1B1C1D1,O1,O2分别是正方形ABB1A1、DCC1D1的对角线的交点,求证:∠A1O1D1=∠CO2B.
如图,在正方体ABCD-A1B1C1D1,O1,O2分别是正方形ABB1A1、DCC1D1的对角线的交点,求证:∠A1O1D1=∠CO2B.