题目内容
如图，在梯形ABCD中，AB∥CD∥EF，若AB=5，CD=2，EF=4，则梯形ABFE与梯形EFDC的面积比是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
考点：平行线分线段成比例定理
专题：计算题,立体几何
分析：过D作DG∥BC交AB于G，交EF于H，根据平行四边形的性质先求出BG=FH=CD，从而得到EH，AG的长，再根据平行线分线段成比例定理可求出梯形ABFE与梯形EFDC的高的比，即可求出梯形ABFE与梯形EFDC的面积比．
解答：
解：过D作DG∥BC交AB于G，交EF于H．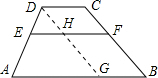
则BG=FH=CD=2，
∴EH=EF-FH=2，AG=3，
∵AB∥EF，
∴DE：AE=2：1，
∴梯形ABFE与梯形EFDC的高的比为1：2，
∴梯形ABFE与梯形EFDC的面积比是
=
故选：D．
则BG=FH=CD=2，
∴EH=EF-FH=2，AG=3，
∵AB∥EF，
∴DE：AE=2：1，
∴梯形ABFE与梯形EFDC的高的比为1：2，
∴梯形ABFE与梯形EFDC的面积比是
| 5+4 |
| (2+4)×2 |
| 3 |
| 4 |
故选：D．
点评：本题考查平行线分线段成比例定理，考查梯形的面积公式是一个基础题，解题的时候容易出的一个错误是把两个梯形看成相似梯形，根据相似多边形的面积之比等于相似比的平方．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
某项活动从甲、乙、丙、丁四人中任选两名参加，甲被选中的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f（x）=lnx+2x-6的零点必定属于区间（ ）
| A、（-2，1） | ||||
B、(
| ||||
C、(1，
| ||||
D、(
|
M（a，b）为圆x2+y2=r2（r＞0）内异于圆心的一点，则直线ax+by=r2与该圆的位置关系是（ ）
| A、相切 | B、相交 |
| C、相离 | D、相切或相交 |
二次函数f（x）=ax2+bx+c（x∈R）的部分对应值如下表：
可以判断方程ax2+bx+c=0的两个根所在的区间是（ ）
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | M | -4 | -6 | -6 | -4 | n | 6 |
| A、（-3，-1）和（2，4） |
| B、（-3，-1）和（-1，1） |
| C、（-1，1）和（1，2） |
| D、（-∞，-3）和（4，+∞） |
已知两点A（-1，0），B（0，1），点P是圆C：（x-1）2+y2=1上任意一点，则点P到直线AB的距离d的最大值与最小值分别是（ ）
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
设集合A={1，3}，B={1，2，4，5}，则A∪B=（ ）
| A、{1，2，3，4，5} |
| B、{2，3，4，5} |
| C、{1，3} |
| D、{1} |
下列各组数据中方差最大的是（ ）
| A、2，6，7 |
| B、2，5，8 |
| C、1，6，8 |
| D、1，5，9 |