题目内容
18.在直角坐标系xOy中,曲线C的参数方程为$\left\{\begin{array}{l}{x=2+cosα}\\{y=sinα}\end{array}\right.$ (α为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为ρsin($θ+\frac{π}{4}$)=2$\sqrt{2}$.(I)求曲线C与直线l在该直角坐标系下的普通方程;
(Ⅱ)动点A在曲线C上,动点B在直线l上,定点P(-1,1),求|PB|+|PA|的最小值.
分析 (I)利用同角三角函数的关系消参数α得到曲线C的普通方程,将直线l的极坐标方程按和角公式展开,利用直角坐标与极坐标的对应关系得出直线l的直角坐标方程;
(II)分别求出P点到圆心和直线的距离,得出|PA|和|PB|的最小值.
解答 解:(I)曲线C的直角坐标方程为(x-2)2+y2=1,
∵ρsin($θ+\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$ρsinθ+$\frac{\sqrt{2}}{2}$ρcosθ=2$\sqrt{2}$.
∴ρsinx+ρcosx=4,
∴直线l的直角坐标方程为x+y-4=0.
(II)曲线C的半径r=1,圆心为(2,0).
∴曲线C的圆心C(2,0)到P点的距离d=$\sqrt{(2+1)^{2}+(0-1)^{2}}=\sqrt{10}$,
∴|PA|的最小值为d-r=$\sqrt{10}$-1.
点P(-1,1)到直线l的距离d′=$\frac{|2-4|}{\sqrt{2}}=\sqrt{2}$,
∴|PB|的最小值为$\sqrt{2}$.
∴|PB|+|PA|的最小值为$\sqrt{10}+\sqrt{2}-1$.
点评 本题考查了参数方程,极坐标方程与普通方程的转化,距离公式的应用,属于基础题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
8.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线的斜率为-2,则C的离心率e=( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | 2 | D. | $\sqrt{5}$ |
10.阅读如图的程序框图,当该程序运行后输出的x值是( )
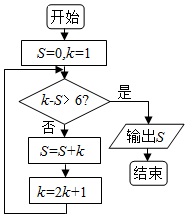

| A. | 57 | B. | 63 | C. | 110 | D. | 120 |
7.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)两条渐近线的夹角为60°,则该双曲线的离心率为( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{{2\sqrt{3}}}{3}$或2 | D. | 4 |