题目内容
7.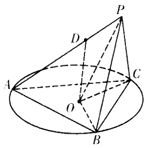 如图所示,正三角形ABC的外接圆半径为2,圆心为O,PB=PC=2,D为AP上一点,AD=2DP,点D在平面ABC内的射影为圆心O.
如图所示,正三角形ABC的外接圆半径为2,圆心为O,PB=PC=2,D为AP上一点,AD=2DP,点D在平面ABC内的射影为圆心O.(Ⅰ)求证:DO∥平面PBC;
(Ⅱ)求三棱锥O-PBC的体积.
分析 (Ⅰ)由O为正三角形ABC的外接圆圆心,知O是三角形ABC的中心,连接AO并延长,交BC于E,则AO=2OE,连接PE,又已知AD=2DP,结合平行线截线段成比例定理可得OD∥PE,再由线面平行的判定可得OD∥平面PBC;
(Ⅱ)由正三角形ABC的外接圆半径为2,求出正三角形边长,再由PB=PC=2求得PE,利用等积法求得三棱锥O-PBC的体积.
解答 (Ⅰ)证明:如图,
∵O为正三角形ABC的外接圆圆心,∴O是三角形ABC的中心,
连接AO并延长,交BC于E,则AO=2OE,连接PE,
又AD=2DP,
∴OD∥PE,
∵PE?平面PBC,OD?平面PBC,
∴OD∥平面PBC;
(Ⅱ)解:∵正三角形ABC的外接圆半径为2,即OA=2,
∴AE=3,则BE=$\sqrt{3}$,
∴${S}_{△ABC}=3\sqrt{3}$,${S}_{△BOC}=\frac{1}{3}{S}_{△ABC}=\sqrt{3}$.
∵OD⊥平面ABC,PE∥OD,
∴PE⊥平面ABC,
又PB=PC=2,BE=$\sqrt{3}$,
∴PE=1.
则VO-PBC=VP-OBC=$\frac{1}{3}×{S}_{△OBC}×PE=\frac{1}{3}×\sqrt{3}×1=\frac{\sqrt{3}}{3}$.
点评 本题考查线面平行的判定,考查了空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
相关题目
17.已知抛物线x2=2px(p>0)经过点线$M({\frac{1}{2},2})$,则它的准线方程为( )
| A. | $y=-\frac{1}{32}$ | B. | B | C. | C | D. | D |
15.已知a∈R,命题“?x∈(0,+∞),等式lnx=a成立”的否定形式是( )
| A. | ?x∈(0,+∞),等式lnx=a不成立 | B. | ?x∈(-∞,0),等式lnx=a不成立 | ||
| C. | ?x0∈(0,+∞),等式lnx0=a不成立 | D. | ?x0∈(-∞,0),等式lnx0=a不成立 |
 如图所示,正三角形ABC的外接圆半径为2,圆心为O,PB=PC=2,D为AP上一点,AD=2DP,点D在平面ABC内的射影为圆心O.
如图所示,正三角形ABC的外接圆半径为2,圆心为O,PB=PC=2,D为AP上一点,AD=2DP,点D在平面ABC内的射影为圆心O. 如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,BC=1,AB=2,$PC=PD=\sqrt{2}$,E为PA中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,BC=1,AB=2,$PC=PD=\sqrt{2}$,E为PA中点.