题目内容
9．已知M是由满足下述条件的函数构成的集合：对任意f（x）∈M，①方程f（x）-x=0有实数根；②函数f（x）的导数f′（x）满足0＜f′（x）＜1．（Ⅰ）集合M中的元素f（x）具有下面的性质：若f（x）的定义域为D，则对于任意[m，n]⊆D，都存在x0∈（m，n），使得等式f（n）-f（m）=（n-m）f′（x0）成立．试用这一性质证明：方程f（x）-x=0有且只有一个实数根；
（Ⅱ）对任意f（x）∈M，且x∈（a，b），求证：对于f（x）定义域中任意的x1，x2，x3，当|x2-x1|＜1，且|x3-x1|＜1时，|f（x3）-f（x2）|＜2．
分析 （Ⅰ）假设方程f（x）-x=0存在两个实数根α，β（α≠β），不妨设α＜β，得到f'（c）=1，与已知0＜f'（x）＜1矛盾，假设不成立；
（Ⅱ）求出函数f（x）-x为减函数，得到|f（x3）-f（x2）|＜|x3-x2|，判断出-1＜x1-x2＜1，|x3-x1|＜1和-1＜x3-x1＜1，相加即可．
解答 （Ⅰ）证明：假设方程f（x）-x=0存在两个实数根α，β（α≠β），
则f（α）-α=0，f（β）-β=0．…（2分）
不妨设α＜β，根据题意存在c∈（α，β），
满足f（β）-f（α）=（β-α）f'（c）．
因为f（α）=α，f（β）=β，且α≠β，所以f'（c）=1．…（5分）
与已知0＜f'（x）＜1矛盾．又f（x）-x=0有实数根，
所以方程f（x）-x=0有且只有一个实数根．…（6分）
（Ⅱ）解：当x2=x3时，结论显然成立；…（7分）
当x2≠x3，不妨设a＜x2＜x3＜b．
因为x∈（a，b），且f'（x）＞0，所以f（x）为增函数，那么f（x2）＜f（x3）．
又因为f'（x）-1＜0，所以函数f（x）-x为减函数，…（9分）
所以f（x2）-x2＞f（x3）-x3．
所以0＜f（x3）-f（x2）＜x3-x2，即|f（x3）-f（x2）|＜|x3-x2|．…（10分）
因为|x2-x1|＜1，所以-1＜x1-x2＜1，（1）
又因为|x3-x1|＜1，所以-1＜x3-x1＜1，（2）
（1）+（2）得-2＜x2-x3＜2即|x3-x2|＜2．…（12分）
所以|f（x3）-f（x2）|＜|x3-x2|＜2．…（13分）
综上，对于任意符合条件的x1，x2，x3总有|f（x3）-f（x2）|＜2成立．…（14分）
点评 本题考查了新定义问题，考查反证法的应用以及函数的单调性问题，考查绝对值的应用，是一道中档题．
长江作业本同步练习册系列答案
小天才课时作业系列答案
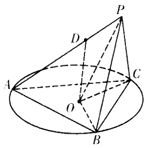如图所示，正三角形ABC的外接圆半径为2，圆心为O，PB=PC=2，D为AP上一点，AD=2DP，点D在平面ABC内的射影为圆心O．| A． | -1 | B． | 0 | C． | 1 | D． | 2 |