题目内容
15.已知抛物线E:y2=2px(p>0)的准线方程为x=-$\frac{1}{16}$.(1)求抛物线的方程;
(2)定长为2的线段MN的两端点在抛物线E上移动,O为坐标原点,点P满足$\frac{\overrightarrow{OM}+\overrightarrow{ON}}{2}$=$\overrightarrow{OP}$,求点P到y轴距离的最小值.
分析 (1)由已知中的准线方程,求出p值,可得抛物线的方程;
(2)先设出M,N的坐标,根据抛物线方程可求得其准线方程,进而可表示出M到y轴距离,根据抛物线的定义结合两边之和大于第三边且A,B,F三点共线时取等号判断出$\frac{|MF|+|NF|}{2}$的最小值即可.
解答 解:(1)∵抛物线E:y2=2px(p>0)的准线方程为x=-$\frac{1}{16}$.
∴$\frac{p}{2}$=$\frac{1}{16}$,
解得:p=$\frac{1}{8}$,
即抛物线E的方程为:y2=$\frac{1}{4}$x;
(2)设M(x1,y1),N(x2,y2),
∵点P满足$\frac{\overrightarrow{OM}+\overrightarrow{ON}}{2}$=$\overrightarrow{OP}$,故P为MN的中点,
P到y轴距离S=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{|MF|+|NF|}{2}$-$\frac{1}{16}$≥$\frac{|MN|}{2}$-$\frac{1}{16}$=1-$\frac{1}{16}$=$\frac{15}{16}$,
当且仅当M,N过F点时取等号,
点评 本小题主要考查抛物线的简单性质、利用不等式求最值等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
6. 如图,线段AB在平面α内,线段AC⊥α,线段BD⊥AB,且AB=1,AC=BD=4,BD与α所成角的正弦值为$\frac{1}{4}$,则CD=( )
如图,线段AB在平面α内,线段AC⊥α,线段BD⊥AB,且AB=1,AC=BD=4,BD与α所成角的正弦值为$\frac{1}{4}$,则CD=( )
 如图,线段AB在平面α内,线段AC⊥α,线段BD⊥AB,且AB=1,AC=BD=4,BD与α所成角的正弦值为$\frac{1}{4}$,则CD=( )
如图,线段AB在平面α内,线段AC⊥α,线段BD⊥AB,且AB=1,AC=BD=4,BD与α所成角的正弦值为$\frac{1}{4}$,则CD=( )| A. | 5 | B. | $\frac{11}{2}$ | C. | 6 | D. | 7 |
3.若数列{an}满足3an+1=3an+1,则数列是( )
| A. | 公差为1的等差数列 | B. | 公差为$\frac{1}{3}$的等差数列 | ||
| C. | 公差为-$\frac{1}{3}$的等差数列 | D. | 不是等差数列 |
7.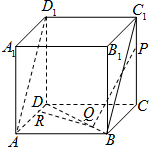 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P、Q分别是线段CC1,BD上的点,R是直线AD上的点,满足PQ∥平面ABC1D1,PQ⊥RQ,则|PR|的最小值是( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P、Q分别是线段CC1,BD上的点,R是直线AD上的点,满足PQ∥平面ABC1D1,PQ⊥RQ,则|PR|的最小值是( )
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P、Q分别是线段CC1,BD上的点,R是直线AD上的点,满足PQ∥平面ABC1D1,PQ⊥RQ,则|PR|的最小值是( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P、Q分别是线段CC1,BD上的点,R是直线AD上的点,满足PQ∥平面ABC1D1,PQ⊥RQ,则|PR|的最小值是( )| A. | $\frac{\sqrt{42}}{6}$ | B. | $\frac{\sqrt{30}}{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
