题目内容
12.在平面直角坐标系xOy中,M为不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-1≥0}\\{x≤3}\end{array}\right.$所表示的区域上一动点,则直线OM斜率的最小值为( )| A. | 0 | B. | 1 | C. | $-\frac{2}{3}$ | D. | $\frac{4}{3}$ |
分析 作出不等式对应的平面区域,利用线性规划的知识,利用斜率的几何意义即可得到结论.
解答  解:作出不等式组对应的平面区域如图:(阴影部分).
解:作出不等式组对应的平面区域如图:(阴影部分).
由图象可知当点M位于A时,直线的斜率最小,
由$\left\{\begin{array}{l}{x=3}\\{x+y-1=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$,
即A(3,-2),
∴OM的斜率k=-$\frac{2}{3}$,
故直线OM斜率的最小值为$-\frac{2}{3}$
故选:C.
点评 本题主要考查线性规划的应用,结合直线斜率的定义,是解决本题的关键.利用数形结合是解决线性规划题目的常用方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.我县某种蔬菜从二月一日起开始上市,通过市场调查,得到西红柿种植成本Q(单位:元/102kg)与上市时间t(单位:天)的数据如下表:
(1)根据上表数据,从下列函数中选取一个函数描述西红柿种植成本Q与上市时间t的变化关系.Q=at+b,Q=at2+bt+c,Q=a•bt,Q=a•logbt.
(2)利用你选取的函数,求西红柿种植成本最低时的上市天数及最低种植成本.
| 时间t | 50 | 110 | 250 |
| 种植成本Q | 150 | 108 | 150 |
(2)利用你选取的函数,求西红柿种植成本最低时的上市天数及最低种植成本.
7.已知$sinα=\frac{3}{5}$,则$sin(\frac{π}{2}+2α)$=( )
| A. | $-\frac{12}{25}$ | B. | $\frac{7}{25}$ | C. | $\frac{12}{25}$ | D. | $-\frac{7}{25}$ |
17.方程x2+y2-2x+4y+6=0表示的图形为( )
| A. | 一个点 | B. | 一个圆 | C. | 一条直线 | D. | 不存在 |
1.给出下面的程序框图,则输出的结果为( )
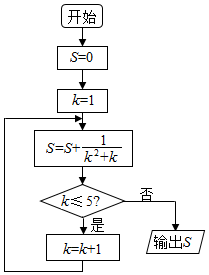

| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{6}{7}$ |
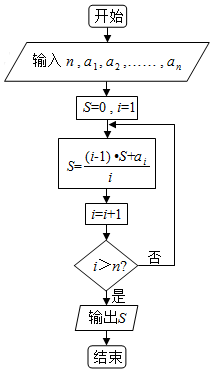 执行如图所示的程序框图,若输入数据n=5,a1=-2,a2=-2.6,a3=3.2,a4=2.5,a5=1.4,则输出的结果为0.5.
执行如图所示的程序框图,若输入数据n=5,a1=-2,a2=-2.6,a3=3.2,a4=2.5,a5=1.4,则输出的结果为0.5.