题目内容
6.已知函数f(x)=ex-kx,x∈R.(1)若k=e,求函数f(x)的单调区间和极值;
(2)若k>0,且对任意x∈R,f(|x|)的图象在x轴上方,求实数k的取值范围.
分析 (1)求出函数的导数,只要解导数的不等式即可,根据导数与0的关系判断函数的单调性;
(2)函数f(|x|)是偶函数,只要f(x)>0对任意x≥0恒成立即可,等价于f(x)在[0,+∞)的最小值大于零.
解答 解:(1)f′(x)=ex-e,令f′(x)=0,解得x=1,
当x∈(1,+∞)时,f′(x)>0,∴f(x)在(1,+∞)单调递增;
当x∈(-∞,1)时,f′(x)<0,∴f(x)在(-∞,1)单调递减.(6分)
(2)∵f(|x|)为偶函数,∴f(|x|)>0恒成立等价于f(x)>0对x≥0恒成立
当x≥0时,f′(x)=ex-k,令f′(x)=0,解得x=lnk,
(1)当lnk>0,即k>1时,f(x)在(0,lnk)减,在(lnk,+∞)增,
∴f(x)min=f(lnk)=k-kllnk>0,解得1<k<e,∴1<k<e,
(2)当lnk≤0,即0<k≤1时,f'(x)=ex-k≥0,∴f(x)在[0,+∞)上单调递增,
∴f(x)min=f(0)=1>0,符合,∴0<k≤1
综上,0<k<e.(12分).
点评 本题考查导数在研究函数的单调性、最值和中的应用,考查等价转化的思想方法以及分析问题的能力.本题的第二问实际上是ex-kx>0在[0,+∞)上恒成立,也可以分离参数构造函数进行解答.

练习册系列答案
相关题目
14.图中阴影部分的面积用定积分表示为( )
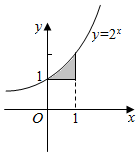
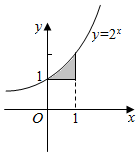
| A. | ${∫}_{0}^{1}$2xdx | B. | ${∫}_{0}^{1}$(2x-1)dx | C. | ${∫}_{0}^{1}$(2x+1)dx | D. | ${∫}_{0}^{1}$(1-2x)dx |
11.抛物线y2=2x上与其焦点距离等于3的点的横坐标是( )
| A. | 1 | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
18.若tan α<0,则( )
| A. | sin α<0 | B. | cos α<0 | C. | sin α•cosα<0 | D. | sin α-cos α<0 |
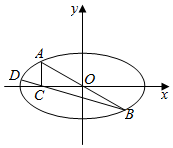 设椭圆M:$\frac{{x}^{2}}{2{c}^{2}}$+$\frac{{y}^{2}}{{c}^{2}}$=1,其中c>0.
设椭圆M:$\frac{{x}^{2}}{2{c}^{2}}$+$\frac{{y}^{2}}{{c}^{2}}$=1,其中c>0.