题目内容
14.设数列{an}的前n项和为Sn.若a2=12,Sn=kn2-1(n∈N*),则数列{$\frac{1}{{S}_{n}}$}的前n项和为$\frac{n}{2n+1}$.分析 Sn=kn2-1(n∈N*),可得:当n≥2时,an=Sn-Sn-1,由a2=12,解得k=4.可得Sn=4n2-1,$\frac{1}{{S}_{n}}$=$\frac{1}{4{n}^{2}-1}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$.利用“裂项求和”即可得出.
解答 解:∵Sn=kn2-1(n∈N*),
∴当n≥2时,an=Sn-Sn-1=kn2-1-[k(n-1)2-1]=2nk-k,
∴a2=4k-k=12,解得k=4.
∴Sn=4n2-1,
∴$\frac{1}{{S}_{n}}$=$\frac{1}{4{n}^{2}-1}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$.
∴数列{$\frac{1}{{S}_{n}}$}的前n项和=$\frac{1}{2}[(1-\frac{1}{3})$+$(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{2n-1}-\frac{1}{2n+1})]$
=$\frac{1}{2}(1-\frac{1}{2n+1})$
=$\frac{n}{2n+1}$.
故答案为:$\frac{n}{2n+1}$.
点评 本题考查了“裂项求和”、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知复数$z=\frac{{1+2{i^3}}}{2+i}$(i为虚数单位),则z在复平面内所对应点的坐标为( )
| A. | (1,0) | B. | (-1,0) | C. | (0,1) | D. | (0,-1) |
14.已知随机变量ξ服从正态分布N(1,δ2),P(ξ≤-1)=0.012,则P(1<ξ<3)=( )
| A. | 0.488 | B. | 0.494 | C. | 0.502 | D. | 0.512 |
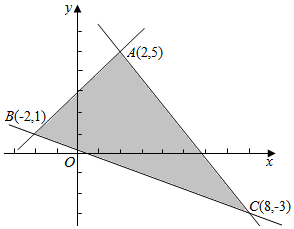 直线l1,l2,l3相交于A(2,5),B(-2,1),C(8,-3).如图所示:
直线l1,l2,l3相交于A(2,5),B(-2,1),C(8,-3).如图所示: