题目内容
已知点P在直线x+3y-1=0上,点Q在直线x+3y+3=0上,PQ中点为M(x0,y0),且y0≥x0+2,则
的取值范围为( )
| y0 |
| x0 |
A、(-
| ||||
B、(-∞,-
| ||||
C、(-
| ||||
D、(-
|
考点:直线的斜率
专题:直线与圆
分析:设出P点坐标及),
=k由M为PQ中点根据中点坐标公式表示出Q的坐标,然后把P和Q分别代入到相应的直线方程中联立可得M的横坐标,因为y0≥x0+2,把解出的M横坐标代入即可得到关于k的不等式,求出解集即可.
| y0 |
| x0 |
解答:
解:设P(x1,y1),
=k,则y0=kx0,∵PQ中点为M(x0,y0),∴Q(2x0-x1,2y0-y1)
∵P,Q分别在直线x+3y-1=0和x+3y+3=0上,
∴x1+3y1-1=0,2x0-x1+3(2y0-y1)+3=0,
∴2x0+6y0+2=0即x0+3y0+1=0,
∵y0=kx0,
∴x0+3kx0+1=0,
∴x0=-
,
又∵y0≥x0+2,代入得kx0≥x0+2,即(k-1)x0≥2即(k-1)(-
)≥2解得-
<k≤-
故选D
| y0 |
| x0 |
∵P,Q分别在直线x+3y-1=0和x+3y+3=0上,
∴x1+3y1-1=0,2x0-x1+3(2y0-y1)+3=0,
∴2x0+6y0+2=0即x0+3y0+1=0,
∵y0=kx0,
∴x0+3kx0+1=0,
∴x0=-
| 1 |
| 1+3k |
又∵y0≥x0+2,代入得kx0≥x0+2,即(k-1)x0≥2即(k-1)(-
| 1 |
| 1+3k |
| 1 |
| 3 |
| 1 |
| 7 |
故选D
点评:本题为中档题,要求学生会利用解析法求出中点坐标,会利用条件列出不等式求解,学生做题时注意灵活变换不等式y0≥x0+2.

练习册系列答案
相关题目
非零实数x、y、z成等差数列,x+1、y、z与x、y、z+2均成等比数列,则y等于( )
| A、16 | B、14 | C、12 | D、10 |
在△ABC中,D是BC边上的一点,
=λ(
+
).|
|=2,|
=4,若记
=
,
=
,则用
,
表示
所得的结果为( )
| AD |
| ||
|
|
| ||
|
|
| AB |
| AC| |
| AB |
| a |
| AC |
| b |
| a |
| b |
| BD |
A、
| ||||||||
B、
| ||||||||
C、-
| ||||||||
D、
|
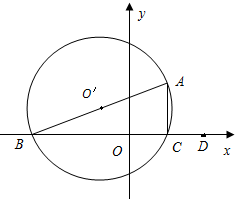 如图,在平面直角坐标系中,△ABC内接于⊙O,其中AB为⊙O直径,A(1,3),B(-3,0),C(1,0).
如图,在平面直角坐标系中,△ABC内接于⊙O,其中AB为⊙O直径,A(1,3),B(-3,0),C(1,0).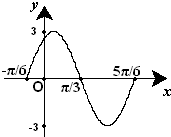 已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的一段图象(如图)所示.
已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的一段图象(如图)所示.