题目内容
半径为1的球内最大圆柱的体积为 .
考点:球内接多面体
专题:计算题,空间位置关系与距离
分析:由题意设圆柱的底面半径为x,高为y,则(2x)2+y2=4,(0<y<2);V=πx2y=π
y=
(4-y2)y,利用导数求最值.
| 4-y2 |
| 4 |
| π |
| 4 |
解答:
解:设圆柱的底面半径为x,高为y,
则(2x)2+y2=4,(0<y<2);
V=πx2y=π
•y
=
(4-y2)y
=
(4y-y3),
则V′=
(4-3y2),
故4-3y2=0,即y=
时,有最大值,
Vmax=
(4-
)
=
.
故答案为:
.
则(2x)2+y2=4,(0<y<2);
V=πx2y=π
| 4-y2 |
| 4 |
=
| π |
| 4 |
=
| π |
| 4 |
则V′=
| π |
| 4 |
故4-3y2=0,即y=
2
| ||
| 3 |
Vmax=
| π |
| 4 |
| 4 |
| 3 |
2
| ||
| 3 |
4π
| ||
| 9 |
故答案为:
4π
| ||
| 9 |
点评:本题考查了学生的空间想象力与导数的综合运用,属于中档题.

练习册系列答案
相关题目
已知集合A={y|y=log3x,x>1},B={y|y=(
)x,x>1},则A∩B=( )
| 1 |
| 3 |
A、{y |0<y<
| ||
| B、{y|0<y<1} | ||
C、{y |
| ||
| D、∅ |
已知点P在直线x+3y-1=0上,点Q在直线x+3y+3=0上,PQ中点为M(x0,y0),且y0≥x0+2,则
的取值范围为( )
| y0 |
| x0 |
A、(-
| ||||
B、(-∞,-
| ||||
C、(-
| ||||
D、(-
|
设y=f(x)是奇函数,则y=f(x)+1( )
| A、是奇函数 |
| B、是偶函数 |
| C、既是奇函数又是偶函数 |
| D、是非奇非偶函数 |
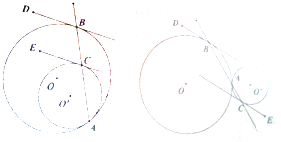 已知:如图,⊙O和⊙O′相切于点A,直线AB和⊙O的另一个交点为B,和⊙O′的另一个交点为C,BD,CE分别切⊙O′,⊙O于点B,C.求证:BD∥CE.研究:两圆外切时结论还成立吗?
已知:如图,⊙O和⊙O′相切于点A,直线AB和⊙O的另一个交点为B,和⊙O′的另一个交点为C,BD,CE分别切⊙O′,⊙O于点B,C.求证:BD∥CE.研究:两圆外切时结论还成立吗?