题目内容
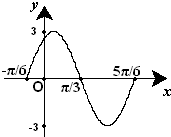 已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的一段图象(如图)所示.
已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的一段图象(如图)所示.(1)求函数的解析式;
(2)写出这个函数的单调增区间;
(3)若x∈[-
| π |
| 6 |
| π |
| 3 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的单调性
专题:三角函数的图像与性质
分析:(1)由图易知A=3,T=
=π,可求得ω=2,利用五点作图法可知,2×(-
)+φ=0,可求得φ,于是可得函数的解析式;
(2)由2kπ-
≤2x+
≤2kπ-
(k∈Z)即可求得函数f(x)=3sin(2x+
)的单调递增区间;
(3)x∈[-
,
]⇒(2x+
)∈[0,π],利用正弦函数的单调性质及最值即可求得m的值,继而可求得函数g(x)的最大值及取得最大值时x的取值.
| 2π |
| ω |
| π |
| 6 |
(2)由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
(3)x∈[-
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
解答:
解:(1)由图可知,A=3,T=
=
-(-
)=π,故ω=2;
由五点作图法可知,2×(-
)+φ=0,
所以,φ=
,满足,|
|<π,
所以f(x)=3sin(2x+
);
(2)由2kπ-
≤2x+
≤2kπ-
(k∈Z)得:kπ-
≤x≤kπ+
(k∈Z),
所以函数f(x)=3sin(2x+
)的单调递增区间为:[kπ-
,kπ+
](k∈Z);
(3)x∈[-
,
]⇒(2x+
)∈[0,π]⇒f(x)=3sin(2x+
)∈[0,3],
故g(x)=f(x)+m∈[m,m+3],
因为x∈[-
,
]时,g(x)min=2,所以m=2,
所以,g(x)max=m+3=5,此时2x+
=
,x=
.
| 2π |
| ω |
| 5π |
| 6 |
| π |
| 6 |
由五点作图法可知,2×(-
| π |
| 6 |
所以,φ=
| π |
| 3 |
| π |
| 3 |
所以f(x)=3sin(2x+
| π |
| 3 |
(2)由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
所以函数f(x)=3sin(2x+
| π |
| 3 |
| 5π |
| 12 |
| π |
| 12 |
(3)x∈[-
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
故g(x)=f(x)+m∈[m,m+3],
因为x∈[-
| π |
| 6 |
| π |
| 3 |
所以,g(x)max=m+3=5,此时2x+
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,着重考查正弦函数的单调性与最值,考查运算求解能力.

练习册系列答案
相关题目
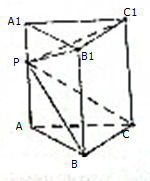 如图所示,点P为三棱柱ABC-A1B1C1侧棱AA1上一动点,若四棱锥P-BCC1B1的体积为V,则三棱柱ABC-A1B1C1的体积为( )
如图所示,点P为三棱柱ABC-A1B1C1侧棱AA1上一动点,若四棱锥P-BCC1B1的体积为V,则三棱柱ABC-A1B1C1的体积为( )| A、2V | ||
| B、3V | ||
C、
| ||
D、
|
已知点P在直线x+3y-1=0上,点Q在直线x+3y+3=0上,PQ中点为M(x0,y0),且y0≥x0+2,则
的取值范围为( )
| y0 |
| x0 |
A、(-
| ||||
B、(-∞,-
| ||||
C、(-
| ||||
D、(-
|