题目内容
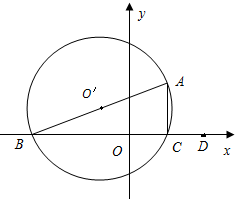 如图,在平面直角坐标系中,△ABC内接于⊙O,其中AB为⊙O直径,A(1,3),B(-3,0),C(1,0).
如图,在平面直角坐标系中,△ABC内接于⊙O,其中AB为⊙O直径,A(1,3),B(-3,0),C(1,0).(1)请在x轴上找一点D,使得△BDA与△BAC相似(不包含全等),并求出点D的坐标;
(2)在(1)的条件下,如果P,Q分别是BA,BD上的动点,连接PQ,设BP=DQ=m.问是否存在这样的m,使得△BPQ与△BDA相似?若存在,求出m的值;若不存在,请说明理由.
考点:直线和圆的方程的应用
专题:计算题,直线与圆
分析:(1)根据条件先判断△ABD中,∠BAD为直角,再由三角形相似的性质可得,对应边成比例,即可解得D的坐标;
(2)假设存在这样的m,使得△BPQ与△BDA相似.运用相似的性质对应边成比例,得到m的方程,解得即可判断.
(2)假设存在这样的m,使得△BPQ与△BDA相似.运用相似的性质对应边成比例,得到m的方程,解得即可判断.
解答:
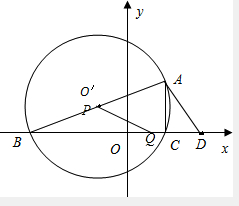 解:(1)由于△ABC为直角三角形,且C为直角,
解:(1)由于△ABC为直角三角形,且C为直角,
则△ABD中,∠BAD为直角,
由△BCA∽△BAD,即有
=
=
,则BD=
=
,则D的坐标为(
-3,0)即(
,0);
(2)假设存在这样的m,使得△BPQ与△BDA相似.
则
=
=
,
由于BP=DQ=m,则
=
=
,解得,m=
,
PQ=
,满足BP2=BQ2+PQ2,成立.
故存在这样的m,且m=
,使得△BPQ与△BDA相似.
 解:(1)由于△ABC为直角三角形,且C为直角,
解:(1)由于△ABC为直角三角形,且C为直角,则△ABD中,∠BAD为直角,
由△BCA∽△BAD,即有
| BC |
| BA |
| BA |
| BD |
| CA |
| AD |
| BA2 |
| BC |
=
| 25 |
| 4 |
| 25 |
| 4 |
| 13 |
| 4 |
(2)假设存在这样的m,使得△BPQ与△BDA相似.
则
| BP |
| BD |
| PQ |
| DA |
| BQ |
| BA |
由于BP=DQ=m,则
| m | ||
|
| PQ | ||
|
| ||
| 5 |
| 125 |
| 36 |
PQ=
| 25 |
| 12 |
故存在这样的m,且m=
| 125 |
| 36 |
点评:本题考查主要考查三角形的相似的判定和性质,考查运算能力,属于中档题.

练习册系列答案
相关题目
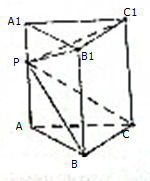 如图所示,点P为三棱柱ABC-A1B1C1侧棱AA1上一动点,若四棱锥P-BCC1B1的体积为V,则三棱柱ABC-A1B1C1的体积为( )
如图所示,点P为三棱柱ABC-A1B1C1侧棱AA1上一动点,若四棱锥P-BCC1B1的体积为V,则三棱柱ABC-A1B1C1的体积为( )| A、2V | ||
| B、3V | ||
C、
| ||
D、
|
已知点P在直线x+3y-1=0上,点Q在直线x+3y+3=0上,PQ中点为M(x0,y0),且y0≥x0+2,则
的取值范围为( )
| y0 |
| x0 |
A、(-
| ||||
B、(-∞,-
| ||||
C、(-
| ||||
D、(-
|
下列函数中,既是偶函数又在区间(-∞,0)上单调递增的是( )
A、f(x)=
| ||
| B、f(x)=x2+1 | ||
| C、f(x)=x3 | ||
| D、f(x)=2-x |