cos35°cos25°-sin145°cos65°的值为( )A．-$\frac{1}{2}$B．cos10°C．$\frac{1}{2}$D．-cos10° 题目和参考答案——青夏教育精英家教网—

题目内容

13．cos35°cos25°-sin145°cos65°的值为（　　）

A．

-$\frac{1}{2}$

B．

cos10°

C．

$\frac{1}{2}$

D．

-cos10°

分析利用诱导公式把要求的式子化为cos35°cos25°-sin35°sin25°，再利用两角和的余弦公式化为cos60°，从而得到结论．

解答解：cos35°cos25°-sin145°cos65°=cos35°cos25°-sin35°sin25°=cos（35°+25°）=$\frac{1}{2}$，
故选：C

点评本题主要考查诱导公式、两角和余弦公式的应用，注意公式的逆用，属于基本知识的考查．

练习册系列答案

4．已知平面内有A（-2，1），B（1，4），使$\overrightarrow{AC}$=$\frac{1}{2}$$\overrightarrow{CB}$成立的点C坐标为（-1，2）．

1．已知函数f（x）=2x²-（m²+m+1）x+15，g（x）=m²x-m，其中m∈R．
（1）若f（x）+g（x）+m≥0，对x∈[1，4）恒成立，求实数m的取值范围；
（2）设函数$F（x）=\left\{{\begin{array}{l}{g（x），x≥0}\\{f（x），x＜0}\end{array}}\right.$
①对任意的x₁＞0，存在唯一的实数x₂＜0，使其F（x₁）=F（x₂），求m的取值范围；
②是否存在求实数m，对任意给定的非零实数x₁，存在唯一非零实数x₂（x₁≠x₂），使其F（x₂）=F（x₁），若存在，求出m的值；若不存在，请说明理由．

8．已知m∈R，函数f（x）=$\left\{\begin{array}{l}|2x+1|，x＜1\\ ln（x-1），x＞1\end{array}$，g（x）=x²-2x+2m²-1，若函数y=f（g（x））-m有6个零点则实数m的取值范围是$（0，\frac{3}{4}）$．

18．将号码分别为1，2，3，4的四个小球放入一个袋中，这些小球仅号码不同，其余完全相同，甲从袋中摸出一个小球，其号码为a，放回后，乙从此袋中再摸出一个小球，其号码为b，则使不等式a-2b+4＜0成立的事件发生的概率为（　　）

5．

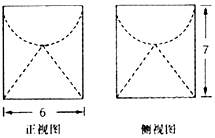某几何体由圆柱挖掉半个球和一个圆锥所得，三视图中的正视图和侧视图如图所示，求该几何体的表面积（　　）

2．已知函数f（x）=alnx-bx²，a，b∈R．若f（x）在x=1处与直线y=-$\frac{1}{2}$相切．
（1）求a，b的值；
（2）求f（x）在[$\frac{1}{e}$，e]上的最大值．

3．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$，一个顶点为A（2，0），离心率为$\frac{{\sqrt{2}}}{2}$，直线y=k（x-1）与椭圆C交于不同的两点M、N两点．
（1）求椭圆C的方程；
（2）当△AMN的面积为$\frac{{4\sqrt{2}}}{5}$时，求k的值．

试题分类