题目内容
5．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的焦距为2$\sqrt{5}$，且双曲线的一条渐近线与直线2x+y=0垂直，则双曲线的顶点到渐近线的距离为（ ）| A． | 1 | B． | 2 | C． | $\frac{2\sqrt{5}}{5}$ | D． | $\frac{4\sqrt{5}}{5}$ |
分析 利用已知条件列出方程求出双曲线的几何量，a，b，c，然后求解双曲线的顶点到渐近线的距离．
解答 解：双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的焦距为2$\sqrt{5}$，且双曲线的一条渐近线与直线2x+y=0垂直，
可得c=$\sqrt{5}$，$\frac{b}{a}$=$\frac{1}{2}$，a2+b2=5，解得a=2，b=1，
双曲线的顶点（2，0）到渐近线x+2y=0的距离为：$\frac{2}{\sqrt{{1}^{2}+{2}^{2}}}$=$\frac{2\sqrt{5}}{5}$．
故选：C．
点评 本题考查双曲线的方程的求法，双曲线的简单性质的应用，考查计算能力．
练习册系列答案
名校课堂系列答案
相关题目
6．设向量$\overrightarrow a，\overrightarrow b$满足$|{\overrightarrow a}|=2\sqrt{2}，|{\overrightarrow b}|=\sqrt{2}$，且$\overrightarrow a•\overrightarrow b=1$，则$|{\overrightarrow a-2\overrightarrow b}|$=（ ）
| A． | $2\sqrt{3}$ | B． | 12 | C． | $2\sqrt{2}$ | D． | 8 |
16．设m、n是两条不同的直线，α、β、γ是三个不同的平面，给出下列四个命题：
①若m∥n，n?α，则m∥α
②若m⊥α，m∥β，则α⊥β
③α∥β，α∥γ，则β∥γ
④若α⊥β，m∥α，则m⊥β
其中正确命题的序号是（ ）
①若m∥n，n?α，则m∥α
②若m⊥α，m∥β，则α⊥β
③α∥β，α∥γ，则β∥γ
④若α⊥β，m∥α，则m⊥β
其中正确命题的序号是（ ）
| A． | ①③ | B． | ①④ | C． | ②③ | D． | ②④ |
13．若抛物线y2=2px（p＞0）上一点P（2，y0）到其准线的距离为4，则抛物线的标准方程为（ ）
| A． | y2=2x | B． | y2=4x | C． | y2=6x | D． | y2=8x |
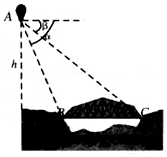如图，从气球A上测得正前方的河流的两岸B、C的俯角分别为α=60°，β=45°，如果此时气球的高度h是10米，则河流的宽度BC=10-$\frac{10\sqrt{3}}{3}$米．