题目内容
20.在平面直角坐标系xOy中,已知直线l:ax+(a2-2)y+3=0与直线m:x-y-1=0互相垂直,其中a>0.(1)求直线l的方程;
(2)点P坐标为(3,-1),求过点P与直线l平行的直线方程.
分析 (1)利用直线垂直关系,求出a,即可求直线l的方程;
(2)设过点P与直线l平行的直线方程为x+y+c=0,代入点,求出c,即可求过点P与直线l平行的直线方程.
解答 解:(1)∵直线l:ax+(a2-2)y+3=0与直线m:x-y-1=0互相垂直,
∴a-a2+2=0,
∵a>0,∴a=2,
∴直线l的方程:2x+2y+3=0;
(2)设过点P与直线l平行的直线方程为x+y+c=0,
(3,-1)代入可得c=-2,∴过点P与直线l平行的直线方程为x+y-2=0.
点评 本题考查直线方程,考查直线与直线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.过点P(-4,0)作函数y=$\sqrt{4-{x}^{2}}$的切线l,则切线l的方程为( )
| A. | y=$\sqrt{3}$(x+4) | B. | y=$\frac{\sqrt{3}}{3}$(x+4) | C. | y=$\frac{\sqrt{2}}{2}$(x+4) | D. | y=$\sqrt{2}$(x+4) |
5.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦距为2$\sqrt{5}$,且双曲线的一条渐近线与直线2x+y=0垂直,则双曲线的顶点到渐近线的距离为( )
| A. | 1 | B. | 2 | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{4\sqrt{5}}{5}$ |
10.已知α,β是相交平面,直线l?平面α,则“l⊥β”是“α⊥β”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
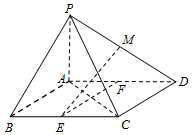 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠ABC=45°,PA⊥底面ABCD,AB=AC=PA=2,E、F分别为BC、AD的中点,点M在线段PD上.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠ABC=45°,PA⊥底面ABCD,AB=AC=PA=2,E、F分别为BC、AD的中点,点M在线段PD上.