题目内容
17.已知各项为正数的数列{an}的前{Sn},满足$\sqrt{2{S_n}}=\frac{{{a_n}+2}}{2}$(Ⅰ)求证:{an}为等差数列,并求其通项公式;
(Ⅱ)设{bn}满足bn+1=2bn,b2=2,求数列{anbn}的前n项和为Tn.
分析 (1)把$\sqrt{2{S_n}}=\frac{{{a_n}+2}}{2}$两边同时平方,然后将n换为n-1,两式相减可以得到(an+an-1)(an-an-1-4)=0,结合{an}的各项均为正数,可得an-an-1=4,即{an}是以4为公差的等差数列,求出a1,代入等差数列的通项公式可得an=4n-2;
(2)依题意,{bn}是以1为首项,2为公比的等比数列,求出 ${b_n}={2^{n-1}}$,代入cn=anbn,然后利用错位相减法求数列{anbn}的前n项和为Tn.
解答 (1)证明:把$\sqrt{2{S_n}}=\frac{{{a_n}+2}}{2}$两边同时平方得,${S_n}=\frac{{{{({a_n}+2)}^2}}}{8},{S_{n-1}}=\frac{{{{({a_{n-1}}+2)}^2}}}{8}$(n≥2),
两式相减可以得到(an+an-1)(an-an-1-4)=0,
∵{an}的各项均为正数,
∴an-an-1-4=0,即an-an-1=4,
故{an}是以4为公差的等差数列.
将n=1代入原式中得a1=2,
∴an=4n-2;
(2)解:依题意,{bn}是以1为首项,2为公比的等比数列,
因此 ${b_n}={2^{n-1}}$,
令cn=anbn,
则Tn=c1+c2+c3+…+cn=(2×1-1)21+(2×2-1)22+(2×3-1)23+…+(2n-1)2n,
两边同乘以2得,$2{T_n}=(2×1-1){2^2}+(2×2-1){2^3}+(2×3-1){2^4}+…+(2n-1){2^{n+1}}$,
两式相减得${T_n}=(2n-3){2^{n+1}}+6$.
点评 本题考查数列递推式,考查了等差关系的确定,训练了错位相减法求数列的前n项和,是中档题.

 阅读快车系列答案
阅读快车系列答案
| A. | -$\frac{{\sqrt{3}}}{3}$ | B. | -$\frac{1}{2}$ | C. | -$\sqrt{3}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |
| A. | 10$\sqrt{2}$ | B. | 20$\sqrt{2}$ | C. | 20$\sqrt{6}$ | D. | $\frac{20\sqrt{6}}{3}$ |
| A. | 1条 | B. | 2条 | C. | 4条 | D. | 6条 |
| A. | 9n-1 | B. | (3n-1)2 | C. | $\frac{1}{2}({{9^n}-1})$ | D. | $\frac{3}{4}({{3^n}-1})$ |
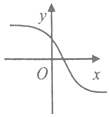
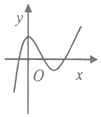
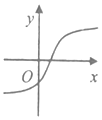
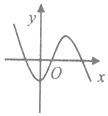
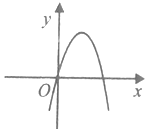 已知函数f(x)的导函数f′(x)=a(x+b)2+c(a≠0)的图象如图所示,则函数f(x)的图象可能是( )
已知函数f(x)的导函数f′(x)=a(x+b)2+c(a≠0)的图象如图所示,则函数f(x)的图象可能是( )