题目内容

如果指数函数f（x）=（a-2）x是R上的减函数，那么a的取值范围是
 
．
考点：指数函数的图像与性质
专题：函数的性质及应用
分析：利用底数大于0小于1时指数函数为减函数，直接求a的取值范围．
解答： 解：∵指数函数y=（a-2）x在x∈R上是减函数
∴0＜a-2＜1⇒2＜a＜3
故答案为：（2，3）．
点评：本题考查指数函数的单调性．指数函数的单调性与底数的取值有关，当底数大于1时指数函数为增函数，当底数大于0小于1时指数函数为减函数
练习册系列答案
相关题目
直线x+
3
y+3=0的倾斜角是（　　）
A、
5
6
π
B、
2
3
π
C、
π
3
D、
π
6
（1）已知x＜
5
4
，求函数y=4x-2+
1
4x-5
的最大值．
（2）已知x＞0，y＞0，且
1
x
+
1
y
=1，求x+y的最小值．
已知实数a≠1，函数f（x）=
4x，x≥0
2a-x，x＜0.
，若f（1-a）=f（a-1），则a的值为
 
．
已知直线l1：ax+y-1=0，直线l2：x-y-3=0，若直线l1的倾斜角为
π
4
，则a=
 
；若l1⊥l2，则a=
 
；若l1∥l2，则两平行直线间的距离为
 
．
设不等式3-2x＜0的解集为M，下列正确的是（　　）
A、0∈M，2∈M
B、0∉M，2∈M
C、0∈M，2∉M
D、0∉M，2∉M
设集合M={y|y=log
1
2
x，0＜x≤
1
4
}，N={y|y=2x，x≤2}．
（1）求M∩N；
（2）记集合A=M∩N，已知B={x|a-1≤x≤5-a，a∈R}，若B⊆A，求a的取值范围．
设集合A={x|-4＜x＜-
1
2
}，B={x|x≤-4}，则A∪（∁RB）=
 
．
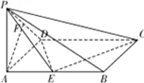已知在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，E、F分别是AB、PD的中点，若二面角P-CD-A为60°，且AD=2，AB=4．
（Ⅰ）求证：AF∥平面PEC；
（Ⅱ）求直线PA与平面PED所成角的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网