题目内容
已知直线l1:ax+y-1=0,直线l2:x-y-3=0,若直线l1的倾斜角为
,则a= ;若l1⊥l2,则a= ;若l1∥l2,则两平行直线间的距离为 .
| π |
| 4 |
考点:两条平行直线间的距离,直线的倾斜角
专题:直线与圆
分析:求出直线的斜率即可求解a,利用直线的垂直,斜率乘积为-1,求解a;通过直线的平行求解a,然后求解平行线之间的距离.
解答:
解:直线l1:ax+y-1=0,直线l2:x-y-3=0,若直线l1的倾斜角为
,k=1,即-a=1,则a=-1:
若l1⊥l2,则-a×1=-1,解得a=1;
若l1∥l2,所以a=-1,则两平行直线间的距离为:
=2
.
故答案为:-1;1;2
.
| π |
| 4 |
若l1⊥l2,则-a×1=-1,解得a=1;
若l1∥l2,所以a=-1,则两平行直线间的距离为:
| |3+1| | ||
|
| 2 |
故答案为:-1;1;2
| 2 |
点评:本题考查直线的垂直,平行,平行线之间的距离求法,考查计算能力.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
计算机中常用16进制,采用数字0~9和字母A~F16个计数符号,与10进制的对应关系如表:那么,16进中的16C化为十进制数应为( )
| 16进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 10进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| A、1612 | B、364 |
| C、5660 | D、360 |
已知全集U=R,A={x|y=
},则∁UA=( )
| 1 | ||
|
| A、[1,+∞) |
| B、(-∞,1) |
| C、(1,+∞) |
| D、(-∞,1] |
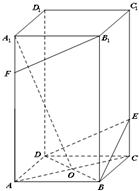 如图,在正四棱柱ABCD-A1B1C1D1中,点O是正方形ABCD对角线的交点,AA1=4,AB=2,点E,F分别在CC1和A1A上,且A1F=CE
如图,在正四棱柱ABCD-A1B1C1D1中,点O是正方形ABCD对角线的交点,AA1=4,AB=2,点E,F分别在CC1和A1A上,且A1F=CE