题目内容
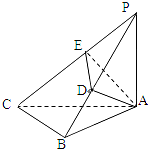 如图,已知PA⊥平面ABC,等腰直角三角形ABC中,AB=BC=2,AB⊥BC,AD⊥PB于D,AE⊥PC于E.
如图,已知PA⊥平面ABC,等腰直角三角形ABC中,AB=BC=2,AB⊥BC,AD⊥PB于D,AE⊥PC于E.(Ⅰ)求证:PC⊥DE;
(Ⅱ)若直线AB与平面ADE所成角的正弦值为
| 2 |
| 3 |
考点:直线与平面所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)先证明BC⊥平面PAB,可得BC⊥AD,证明AD⊥平面PBC,得PC⊥AD,再证明PC⊥平面ADE,即可证明PC⊥DE;
(Ⅱ)过点B作BE∥AP,则BZ⊥平面ABC,分别以BA,BC,BZ所在直线为x轴,y轴,z轴建立空间直角坐标系,根据PC⊥平面ADE,可得
=(-1,1,-a)是平面ADE的一个法向量,从而向量
与
所成的角的余弦值的绝对值为
,即可求PA的值.
(Ⅱ)过点B作BE∥AP,则BZ⊥平面ABC,分别以BA,BC,BZ所在直线为x轴,y轴,z轴建立空间直角坐标系,根据PC⊥平面ADE,可得
| PC |
| PC |
| AB |
| 2 |
| 3 |
解答:
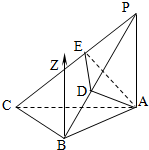 (Ⅰ)证明:因为PA⊥平面ABC,
(Ⅰ)证明:因为PA⊥平面ABC,
所以PA⊥BC,
又AB⊥BC,PA∩AB=A,
所以BC⊥平面PAB,
因为AD?平面PAB,
所以BC⊥AD.…(2分)
又AD⊥PB,BC∩PB=B,
所以AD⊥平面PBC,得PC⊥AD,…(4分)
又PC⊥AE,AD∩AE=A,
所以PC⊥平面ADE,
因为DE?平面ADE,
所以PC⊥DE…(6分)
(Ⅱ)解:过点B作BE∥AP,则BZ⊥平面ABC,如图所示,分别以BA,BC,BZ所在直线为x轴,y轴,z轴建立空间直角坐标系. …(7分)
设PA=a,则A(2,0,0),C(0,2,0),P(2,0,a),
因为PC⊥平面ADE,所以
=(-1,1,-a)是平面ADE的一个法向量,
所以向量
与
所成的角的余弦值的绝对值为
,…(9分)
又
=(-2,0,0)
则|cos<
,
>|=|
|=|
|=
,解得a=1
所以PA=1…(12分)
 (Ⅰ)证明:因为PA⊥平面ABC,
(Ⅰ)证明:因为PA⊥平面ABC,所以PA⊥BC,
又AB⊥BC,PA∩AB=A,
所以BC⊥平面PAB,
因为AD?平面PAB,
所以BC⊥AD.…(2分)
又AD⊥PB,BC∩PB=B,
所以AD⊥平面PBC,得PC⊥AD,…(4分)
又PC⊥AE,AD∩AE=A,
所以PC⊥平面ADE,
因为DE?平面ADE,
所以PC⊥DE…(6分)
(Ⅱ)解:过点B作BE∥AP,则BZ⊥平面ABC,如图所示,分别以BA,BC,BZ所在直线为x轴,y轴,z轴建立空间直角坐标系. …(7分)
设PA=a,则A(2,0,0),C(0,2,0),P(2,0,a),
因为PC⊥平面ADE,所以
| PC |
所以向量
| PC |
| AB |
| 2 |
| 3 |
又
| AB |
则|cos<
| PC |
| AB |
| ||||
|
|
| (-2,2,-a)•(-2,0,0) | ||
|
| 2 |
| 3 |
所以PA=1…(12分)
点评:本题考查线面垂直的判定与性质,考查线面角,考查向量知识的运用,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
已知复数z满足z(1+i)=1(其中i为虚数单位),则z的共轭复数
是( )
. |
| z |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
运行如图所示的程序框图后输出的结果是( )


| A、14 | B、16 | C、18 | D、64 |
 如果执行如图所示的框图,输入如下四个复数:
如果执行如图所示的框图,输入如下四个复数:(1)z=
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
那么输出的复数是( )
| A、(1) | B、(2) |
| C、(3) | D、(4) |
执行如图的程序框图输出的T的值为( )


| A、4 | B、6 | C、8 | D、10 |

 为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.
为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.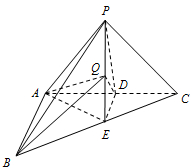 如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC,D,E分别是AC,BC的中点,AB=2
如图,在三棱锥P-ABC中,AB⊥AC,PA=PB=PC,D,E分别是AC,BC的中点,AB=2